T-Tests (R, Python incomplete)

Red means that the page does not exist yet

Gray means that the page doesn’t yet have separation of different levels of understanding

Orange means that the page is started

In this website you can choose to expand or shrink the page to match the level of understanding you want.

  • If you do not expand any (green) subsections then you will only see the most superficial level of description about the statistics. If you expand the green subsections you will get details that are required to complete the tests, but perhaps not all the explanations for why the statistics work.
An example of a green subsection
  • If you expand the blue subsections you will also see some explanations that will give you a more complete understanding. If you are completing MSc-level statistics you would be expected to understand all the blue subsections.
An example of a blue subsection
  • Red subsections will go deeper than what is expected at MSc level, such as testing higher level concepts.
An example of a red subsection

T-tests and ANOVAs

T-tests use the same underlying mathematics as ANOVAs. There is an argument that it’s better to just use the ANOVA mathematics as this will allow you more flexibility in future to do more complex analyses. Expand this for insights into the ANOVA concepts and how they overlap with t-tests.

In the tests below we will frequently come across the following concepts:

Total sum of squares represents all the variance around the mean. We create models to try to explain why data points are different to the mean.

Explained sum of squares represents the variance around the mean that is explained by your model.

Unexplained variance represents whatever variance around the mean that isn’t explained by your model. Sometimes the word residual or error is used to capture the difference between the predicted value of a data point (i.e. what would be explained by the model) and the actual data point (the difference being unexplained).

We summarise this ratio of explained vs. unexplained variance using an F value:

\[ F = \frac{SS_{explained}/df_{explained}}{SS_{unexplained}/df_{unexplained}} \]

  • \(SS_{explained}\) is explained sum of squares

  • \(SS_{unexplained}\) is the unexplained sum of squares

  • \(df_{explained}\) is the degrees of freedom (df) for the model explaining the variance. This is generally the number of levels in your model minus 1. For example, if you were testing if life expectancy is explained by which continent a country is in, then the number of levels is the number of continents in your analysis (e.g. 5 continents), and the df would be 5-1=4. The df is used to address uncertainty because we are using a sample to estimate a population, but you don’t need to understand this to continue on this page.

  • \(df_{unexplained}\) is the degrees of freedom (df) that is not addressed by the model. Generally this is the number of subjects minus 1. Using the above example about continents and life expectancy, each subject could be one of 142 countries in your analysis, and so the df would be 142-1=141.

The key points in the above formula are:

  • The better your model is the more Sum of Squares will be explained, which will increase F

  • The more data points (e.g. subjects) you have, the higher your \(df_{unexplained}\) will be, which will also increase F

On this page we will be focusing on simpler analyses that only compare between 2 conditions, which means \(df_{explained}\) will be (2-1=) 1, which simplifies the above formula:

\[ F = \frac{SS_{explained}/df_{explained}}{SS_{unexplained}/df_{unexplained}} = \frac{SS_{explained}/1}{SS_{unexplained}/df_{unexplained}} = \frac{SS_{explained}}{SS_{unexplained}/df_{unexplained}} \]

This allows us to complete simpler analyses to calculate \(t\) values, which are the square root of \(F\):

\[ t = \sqrt{F} = \sqrt{\frac{SS_{explained}}{SS_{unexplained}/df_{unexplained}}} \]

[probably delete] ANVOA vs. T-test formula

Great. So now that we’ve highlighted the GLM approach works for t-tests, can we see how our formula for a GLM simplifies to the formula we usually use for one-sample t-tests:

\[ T = \sqrt{F} = \sqrt{\frac{SS_{exp}/df_{exp}}{SS_{unexp}/df_{unexp}}} = \sqrt{\frac{N * (\mu - \bar{x})^2/(levelsOfPredictors - 1)}{\sum(x_i-\bar{x})^2/(N-1)}} = \]

\[ \sqrt{\frac{N * (\mu - \bar{x})^2/(2-1)}{\sigma^2}} = \frac{\sqrt{N * (\mu - \bar{x})^2}}{\sqrt{\sigma^2}} = \frac{\sqrt{(\mu - \bar{x})^2}}{\sigma/\sqrt{N}} = \frac{\mu - \bar{x}}{\sigma/\sqrt{N}} \] where:

  • \(T\) is the t-value
  • \(F\) is the f-value
  • \(SS_{exp}\) is the sum of squares of the data explained by the model
  • \(SS_{unexp}\) is the sum of squares of the data not explained by the model (i.e. the residuals)
  • \(df_{exp}\) is the degrees of freedom for the model. As there is only one predictor (the sample mean) and it’s only got 2 levels (1 or 0, however, in all cases the model is comparing the data to the mean, so it’s less intuitive that there are 2 levels).

To confirm, the formula for a one-sample t-test is just:

\[ T = \frac{\mu - \bar{x}}{\sigma/\sqrt{N}} \]

\(t\) values are used for \(t\)-tests, which we’ll address below.

One-sample t-tests

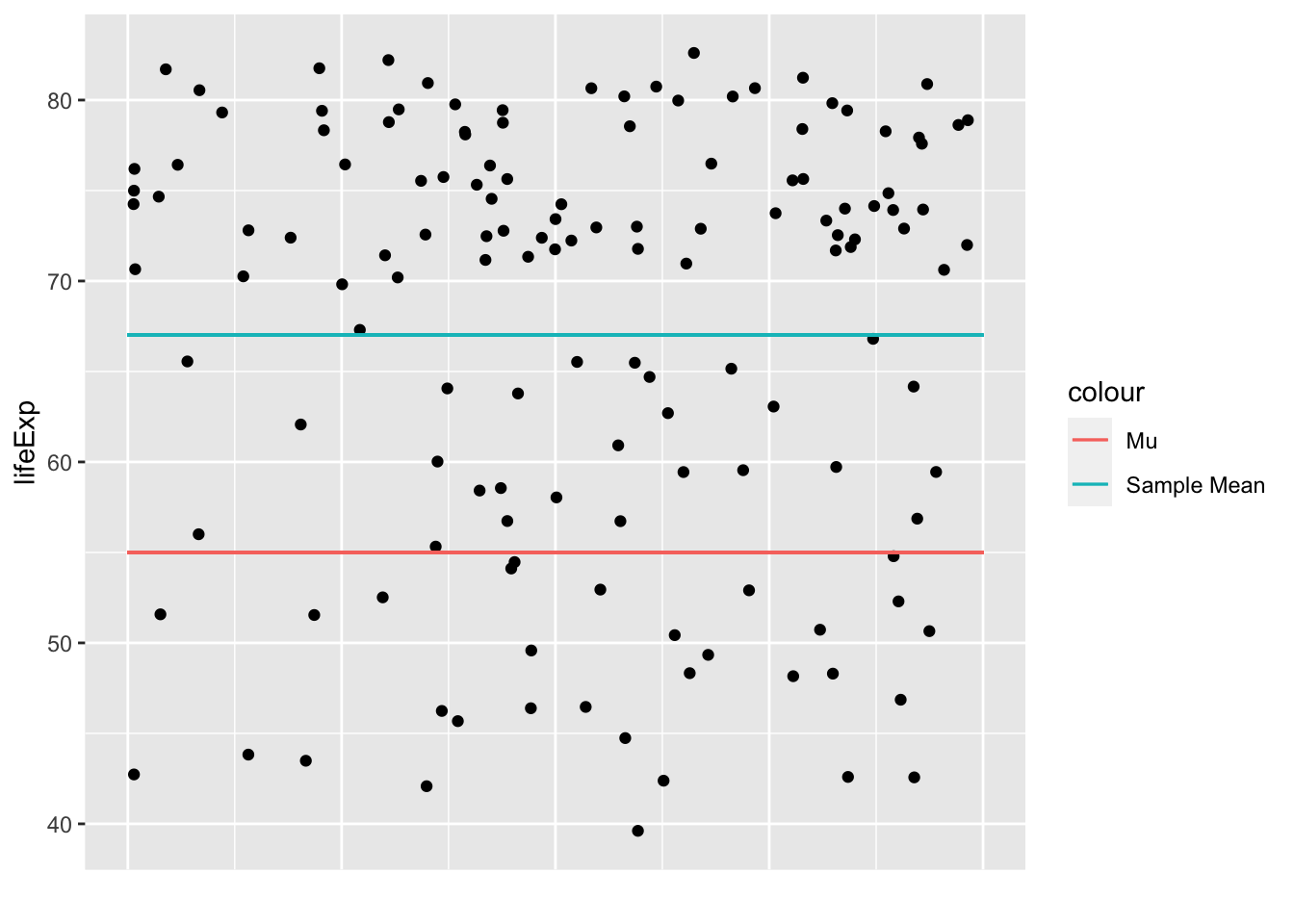
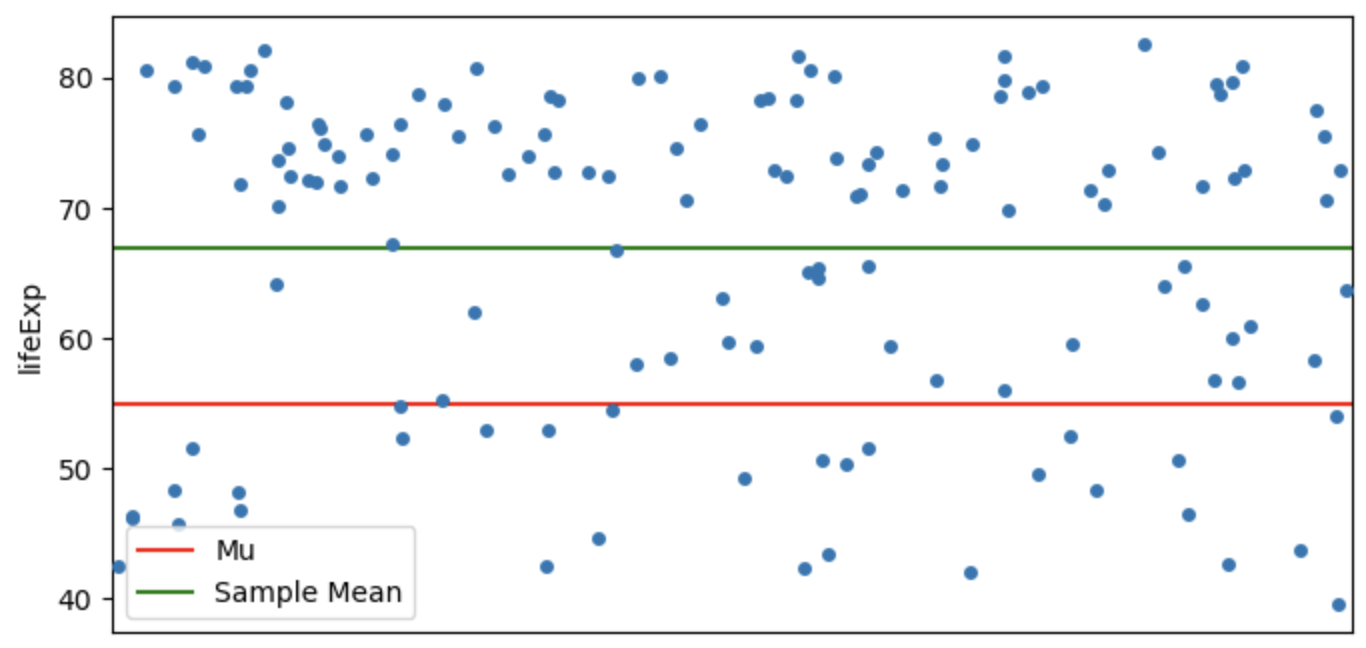
One-sample t-tests test whether your sample’s values are significantly higher or lower than a pre-specified value (\(\mu\)). You can do this by seeing how big the difference is between the mean in your sample (\(\bar{x}\)) and the \(\mu\), when taking into account the general variance in your data and the number of participants you have.

One sample t-tests try to explain whether variance of data is better explained around one specific value (sample mean \(\bar{x}\)) compared to another (previously assumed value \(\mu\)), when compared to the general variance in the data ( \(\sigma/\sqrt{N}\) explained more below).

\[ t_{oneSample}=\frac{\bar{x} - \mu}{\sigma/\sqrt{N} } \]

For example, imagine that you wanted to test whether life expectancy is higher than 55 across the world:

  • Your \(\mu\) would be 55. This can be thought of as the assumed population mean that we want to use our sample to test.

  • Your \(\bar{x}\) would be the sample mean.

Let’s visualise these values using gapminder data from 2007:

Code 
library(ggplot2)
library(gapminder)
gapminder_2007 <- subset(
  gapminder,   # the data set
  year == 2007
)
ggplot(gapminder_2007, aes(x=year,y=lifeExp)) + 
  geom_jitter() + 
  xlab("") + 
  theme(axis.text.x = element_blank()) +
  theme(axis.ticks.x = element_blank()) +
  geom_segment(
    aes(
      x = 2006.6,
      xend = 2007.4,
      y = 55,
      yend = 55,
      color = "Mu"
    )
  ) +
  geom_segment(
    aes(
      x = 2006.6,
      xend = 2007.4,
      y = mean(lifeExp),
      yend = mean(lifeExp),
      color = "Sample Mean"
    )
  )

Code 
# load the gapminder module and import the gapminder dataset
from gapminder import gapminder

# import matplotlib
import matplotlib.pyplot as plt

import seaborn as sns

# create a new data frame that only focuses on data from 2007
gapminder_2007 = gapminder.loc[gapminder['year'] == 2007]

# Create the plot
plt.figure(figsize=(8, 4))

# create the scatterplot with some jitter
sns.stripplot(x="year", y='lifeExp', data=gapminder_2007, dodge=True, jitter=0.5)

# add an horizontal line for Mu
plt.axhline(y=55, color='r', linestyle='-', label='Mu')

# add an horizontal line for the mean of 'lifeExp'
plt.axhline(y=gapminder_2007['lifeExp'].mean(), color='g', linestyle='-', label='Sample Mean')

# remove the label on the x-axis
plt.xlabel("")

# remove the tick on the x-axis
plt.xticks([])

# add the legend 
plt.legend()

# show the plot
plt.show()

Scatterplot with Mu and Sample Mean of ‘Life expectancy’

So the t-value will reflect how significantly higher or lower the sample mean (\(\bar{x}\)) is than the assumed population mean (\(\mu\)). Let’s apply the data from our data to the general formula:

\[ t_{oneSample}=\frac{\bar{x} - \mu}{\sigma/\sqrt{N}} = \frac{67.00742-55}{12.07302/\sqrt{142}} = 11.85163 \]

Let’s confirm that we get the same t-value using a function:

Code 
# t-statistic
t.test(gapminder_2007$lifeExp, mu=55)

    One Sample t-test

data:  gapminder_2007$lifeExp
t = 11.852, df = 141, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 55
95 percent confidence interval:
 65.00450 69.01034
sample estimates:
mean of x 
 67.00742
Code 
from scipy import stats
# Perform a t-test
t_statistic, p_value = stats.ttest_1samp(gapminder_2007['lifeExp'], popmean=55)

print("t-statistic:", t_statistic)
print("p-value:", p_value)
t-statistic: 11.851628442323024
p-value: 6.463174215427706e-23

We can see that the t-value we calculated is the same as calculated by functions (once you take into account rounding numbers). You may have noticed that there is also a p-value associated with t-tests that is very small, suggesting that it is very unlikely that our sample would have such high life expectancy if the \(\mu\) was correct, i.e. if the life expectancy across countries was actually 55 years old. So, the next question you might have is how do we calculate p-values like this using t-values?

Paired samples t-tests

Paired samples t-tests are generally used when you have a group of participants who have completed 2 conditions.

\[ t_{paired} = \frac{\bar{x_1} - \bar{x_2}}{\sigma_{pooled}/\sqrt{N}} \]

! check the above formula !

This is a more powerful analysis than independent samples t-tests because you don’t have noise from the differences between individuals when comparing between the conditions.

FORMULA HERE?

Paired samples t-tests can be approached like 1-sample t-tests, but you first of all need to collapse the data to have a single variable to compare to a \(\mu\) of zero. Let’s do this for gapminder data, comparing life expectancy between 2002 and 2007:

Code 
gapminder_2002_2007_life_exp <- gapminder$lifeExp[gapminder$year == 2007] - gapminder$lifeExp[gapminder$year == 2002]
t.test(gapminder_2002_2007_life_exp, mu = 0)

    One Sample t-test

data:  gapminder_2002_2007_life_exp
t = 14.665, df = 141, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
 1.135561 1.489439
sample estimates:
mean of x 
   1.3125
Code 
gapminder_2002_2007_life_exp = life_exp_2007.reset_index(drop=True) - life_exp_2002.reset_index(drop=True)
t_statistic, p_value = stats.ttest_1samp(gapminder_2002_2007_life_exp, popmean=0)

print("t-statistic:", t_statistic)
print("p-value:", p_value)
t-statistic: 14.664513524875451
p-value: 3.738316746290281e-30

The above suggests that life expectancy was significantly different. Let’s see if we get the exact same value when we use a paired t-test in R:

Code 
t.test(gapminder$lifeExp[gapminder$year == 2007],gapminder$lifeExp[gapminder$year == 2002], paired=T)

    Paired t-test

data:  gapminder$lifeExp[gapminder$year == 2007] and gapminder$lifeExp[gapminder$year == 2002]
t = 14.665, df = 141, p-value < 2.2e-16
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
 1.135561 1.489439
sample estimates:
mean difference 
         1.3125
Code 
# Filter data for the year 2007
life_exp_2007 = gapminder[gapminder['year'] == 2007]['lifeExp']

# Filter data for the year 2002
life_exp_2002 = gapminder[gapminder['year'] == 2002]['lifeExp']

# Perform a paired t-test
t_statistic, p_value = stats.ttest_rel(life_exp_2007, life_exp_2002)

print("T-statistic:", t_statistic)
print("P-value:", p_value)
t-statistic: 14.664513524875451
p-value: 3.738316746290281e-30

Looks identical. Let’s compare formulas to see why this is ( \(\mu\) = 0 , and so it isn’t written) :

\[ t_{paired} = \frac{\bar{x_1} - \bar{x_2}}{\sigma_{pooled}/\sqrt{N}} = \frac{\bar{x_3}}{\sigma_{pooled}/\sqrt{N}} \]

Where

  • \(\bar{x_1}\) is the mean of condition 1

  • \(\bar{x_2}\) is the mean of condition 2

  • \(\bar{x_3}\) is the mean of the result you get when you subtract condition 2 from condition 1 for each participant, i.e. \(mean(x_1-x_2)\).

  • \[ \sigma_{pooled} = \sqrt{\frac{\sigma_1^2 + \sigma_2^2}{2}} OR \frac{\sum(x_1 - x_2)^2}{N-1} \] One way effectively gets the average of the standard deviations of condition and 1. The second way gets the standard deviation of the differences between conditions 1 and 2. Both give you the same outcome.

  • \(N\) is the number of participants

You can rewrite the above formula to compare \(\bar{x_3}\) to \(\mu\), as we know \(\mu\) is zero, which would make this formula (effectively) identical to the one above for one-sample t-tests:

\[ \frac{\bar{x_3} - \mu}{\sigma_{pooled}/\sqrt{N}} \]

The following explains how to calculate F if analysing your data as a model. This isn’t necessary if you just want to complete a t-test, but does help clarify how t-tests overlap with ANOVAs and regressions.

F and value

To calculate the F value we will use the following formula:

\[ F = \frac{SS_{explained}/df_{explained}}{SS_{unexplained}/df_{unexplained}} \]

So the question is, what is our model, and what is explained and what is not explained by it. Our model is that life expectancy is explained by year. We predict that any difference between 2002 and 2007 in life expectancy in any country’s is the mean life expectancy difference across all countries. The sum of squares thus is the mean difference between 2007 and 2002’s life expectancy multiplied by the number of countries:

\[ SS_{explained} = \sum_{country}{{((\bar{lifeExp}_{2007} - \bar{lifeExp}_{2002}})^2)} = ((\bar{lifeExp}_{2007} - \bar{lifeExp}_{2002})^2) * N_{countries} \]

Code 
library(tidyverse)
── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
✔ dplyr     1.1.3     ✔ readr     2.1.4
✔ forcats   1.0.0     ✔ stringr   1.5.0
✔ lubridate 1.9.3     ✔ tibble    3.2.1
✔ purrr     1.0.2     ✔ tidyr     1.3.0
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag()    masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors
Code 
gapminder %>% 
  filter(year == 2007 | year == 2002) -> gapminder_2007_2002
explained_ss = ((mean(gapminder_2007_2002$lifeExp[gapminder_2007_2002$year == 2002]) - mean(gapminder_2007_2002$lifeExp[gapminder_2007_2002$year == 2007]))^2) * length(unique(gapminder_2007_2002$country))
explained_ss
[1] 244.6172

\[ SS_{unexplained} = SS_{total} - SS_{explained} \]

So we need to calculate the total Sum of Squares, which is all variance between 2002 and 2007 for each country (squared):

\[ SS_{total} = \sum{((lifeExp_{2007} - lifeExp_{2002})^2)} \]

Code 
# restructuring data to simplify processing
gapminder_2007_2002 %>% 
  select(country, year, lifeExp) %>% 
  pivot_wider(names_from=year, values_from = lifeExp)  -> gapminder_wide

total_ss = sum((gapminder_wide[["2002"]] - gapminder_wide[["2007"]])^2)
total_ss
[1] 405.0048

To calculate the unexplained variance, let’s subtract the explained from total sum of squares

Code 
unexplained_ss = total_ss - explained_ss
unexplained_ss
[1] 160.3876

Now we can complete the above formula taking into account the explained degrees of freedom is 1 (2 levels -1 = 1), and the unexplained degrees of freedom is 141 (142 countries - 1 = 141):

\[ F = \frac{SS_{explained}/df_{explained}}{SS_{unexplained}/df_{unexplained}} = \frac{244.6172/1}{160.3876/141} = 215.048 \]

Let’s check if this is the same value we get using a function:

Code 
ez::ezANOVA(gapminder_2007_2002, within = year, dv= lifeExp, wid = country)$ANOVA$F
Warning: "year" will be treated as numeric.
Warning: There is at least one numeric within variable, therefore aov() will be
used for computation and no assumption checks will be obtained.
[1] 215.048

Independent Samples t-tests

ANOVA approach

T-tests are restricted to comparisons between 2 conditions/groups, so we will restrict the Gapminder data to allow a comparison between 2 continents. To see if life expectancy was different if you are born in Europe compared to the Americas, let’s first check what the sum of squares is when you just use the mean as the model of life expectancy across these contents (so we’re not separating by continent yet):

Code 
gapminder_americas_europe <- subset(
  gapminder_2007,   # the data set
  continent == "Europe" | continent == "Americas"
)

ggplot(
  gapminder_americas_europe, aes(x=rank(lifeExp), y=lifeExp)
) + 
  geom_point() +
  geom_hline(yintercept = mean(gapminder_americas_europe$lifeExp), color="blue") +
  geom_segment(
    aes(
      xend = rank(lifeExp),
      yend = mean(lifeExp),
      color = "resid"
    )
  ) +
  theme(legend.position = "none")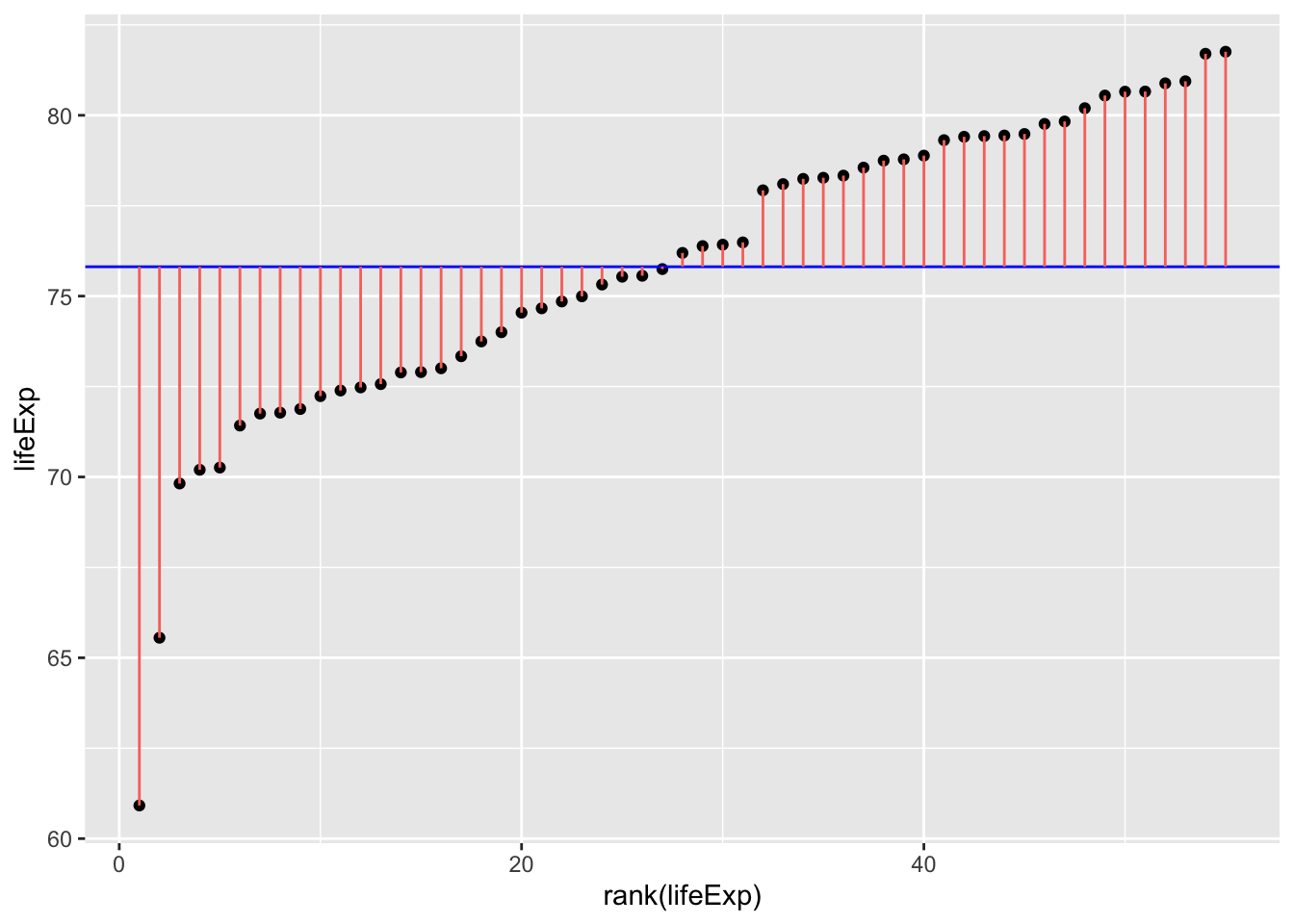

Figure 1: The errors around the mean of life expectancy across Europe and American countries

Code 
gapminder_americas_europe = gapminder_2007.loc[(gapminder_2007['continent'] == "Europe") | (gapminder_2007['continent'] == "Americas")]

gapminder_americas_europe["lifeExp_rank"] = gapminder_americas_europe["lifeExp"].rank()

fig, ax = plt.subplots(figsize =(7, 5))

#scatter plot for the dataset
plt.scatter(gapminder_americas_europe["lifeExp_rank"], gapminder_americas_europe["lifeExp"], color='black', s=10)
# only one line may be specified; full height
plt.axhline(y=gapminder_americas_europe["lifeExp"].mean(), color='blue', ls='-')

plt.vlines(x=gapminder_americas_europe["lifeExp_rank"],ymin=gapminder_americas_europe["lifeExp"], ymax=gapminder_americas_europe["lifeExp"].mean(), colors='red', lw=0.5)

# add title on the x-axis
plt.xlabel("rank(lifeExp)")

# add title on the y-axis
plt.ylabel("lifeExp")

plt.show()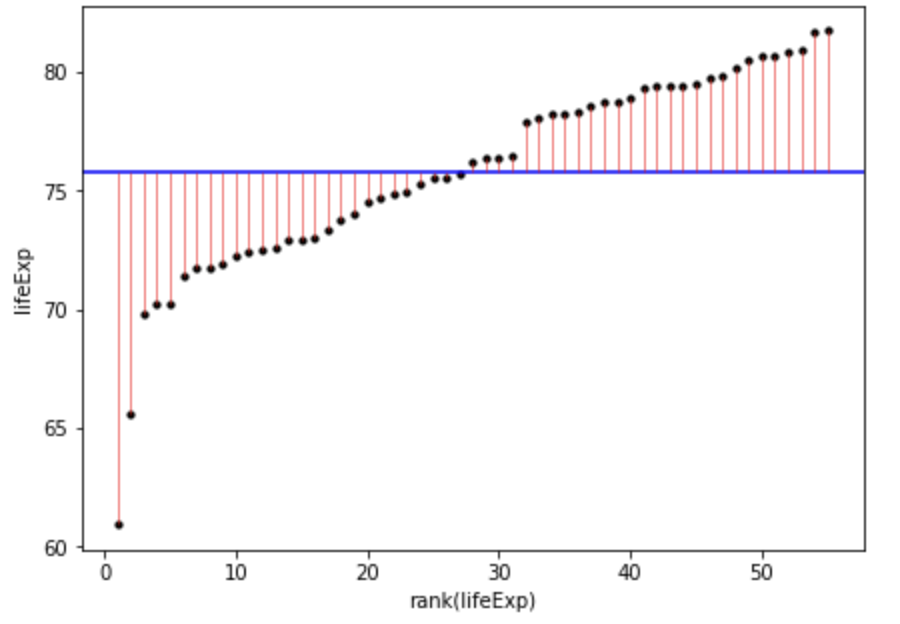

Fig. 3. The errors around the mean of life expectancy across Europe and American countries.

Once we square the errors in the pink lines above, we’ll get the squares:

Code 
ggplot(
  gapminder_americas_europe, 
  aes(
    x=rank(lifeExp), 
    # y is the square of the difference between each data point and the mean across all data poins. Once these are summed you will get the sum of squares.
    y=(lifeExp-mean(lifeExp))^2
  )
) + 
  geom_point() +
  geom_segment(
    aes(
      xend = rank(lifeExp),
      yend = 0,
      color = "resid"
    )
  ) +
  theme(legend.position = "none")

sum((gapminder_americas_europe$lifeExp - mean(gapminder_americas_europe$lifeExp))^2)
[1] 953.4478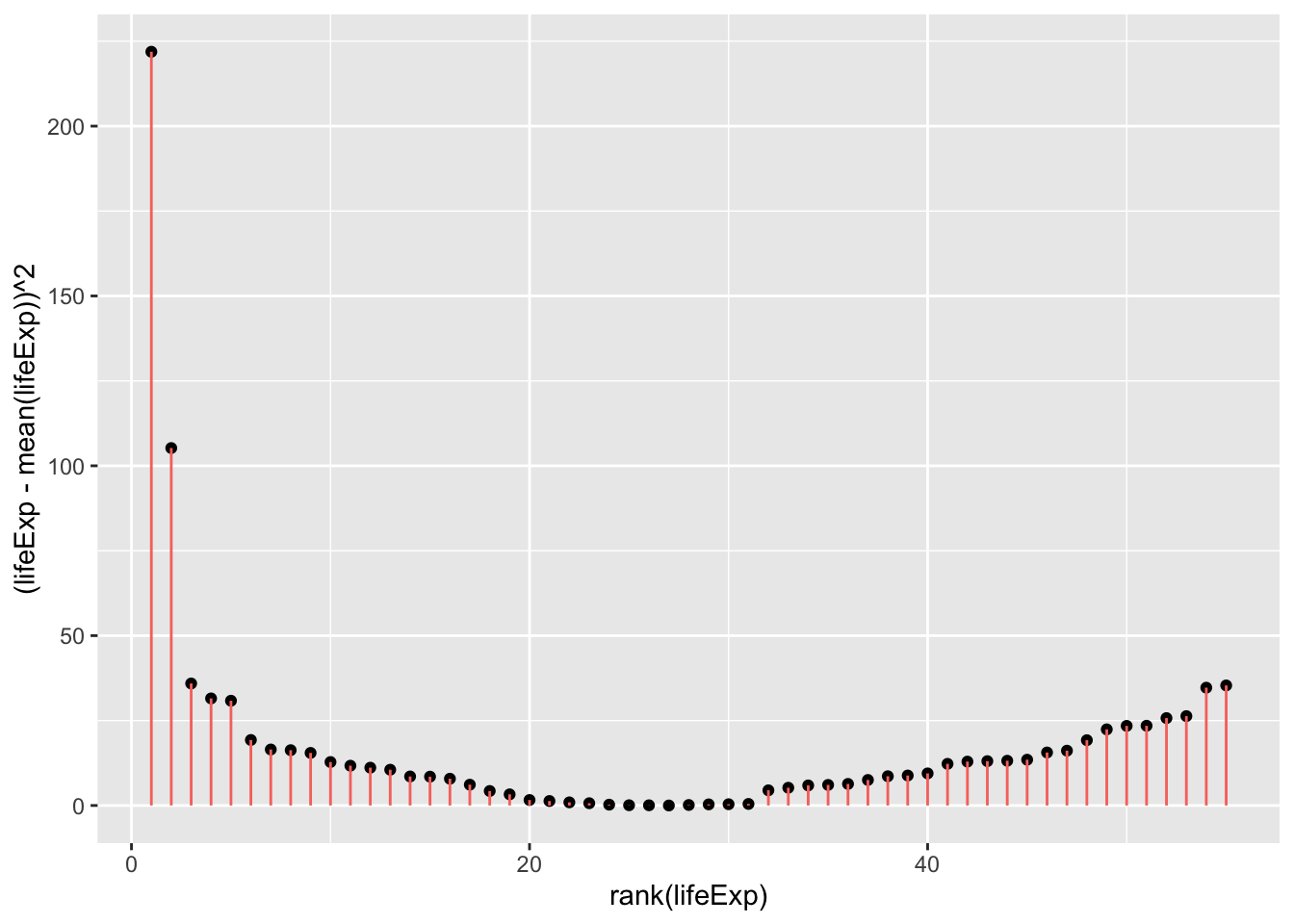

Figure 2: The squared errors around the mean of life expectancy across Europe and American countries

Code 
fig, ax = plt.subplots(figsize =(7, 5))

#scatter plot for the dataset
plt.scatter(gapminder_americas_europe["lifeExp_rank"], (gapminder_americas_europe["lifeExp"]-gapminder_americas_europe["lifeExp"].mean())**2, color='black', s=10)
# only one line may be specified; full height

plt.vlines(x=gapminder_americas_europe["lifeExp_rank"],ymin=0, ymax=(gapminder_americas_europe["lifeExp"]-gapminder_americas_europe["lifeExp"].mean())**2, colors='red', lw=0.5)

# add title on the x-axis
plt.xlabel("rank(lifeExp)")

# add title on the y-axis
plt.ylabel("(Life Expectancy - mean(Life Expectancy))^2")
plt.show()

sum((gapminder_americas_europe["lifeExp"]-gapminder_americas_europe["lifeExp"].mean())**2)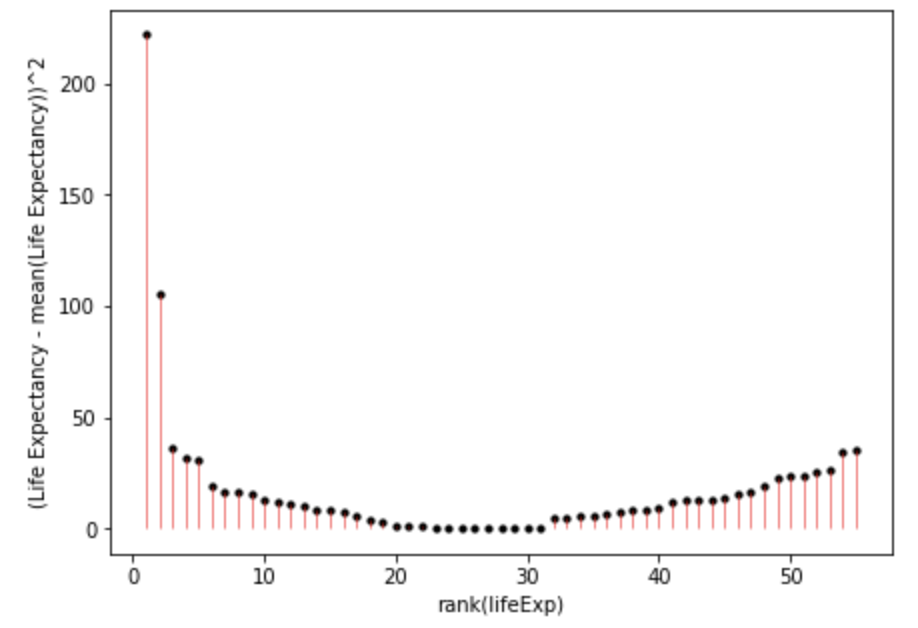

The squared errors around the mean of life expectancy across Europe and American countries

953.4477649818183

And when you add all of these together:

\[ SumOfSquares = \sum(Y_i-\bar{Y})^2 = 953.4478 \]

this should be brought earlier!xs

So the aim is to create models that explain the total sum of squares above.

So if the model we create for a t-test would result in a smaller sum of squares then that suggests it’s a more precise model for estimating life expectancy than simply using the mean as a model. This is because this would mean there’s less error in this model. Let’s model this using a t-test. For this we will need to effect code continent:

Code 
# create a column to place 1 or -1 for each row dependent on the country
contEffect = NA
contEffect[gapminder_americas_europe$continent == "Europe"] = 1
contEffect[gapminder_americas_europe$continent == "Americas"] = -1
gapminder_americas_europe = cbind(contEffect,gapminder_americas_europe)
rmarkdown::paged_table(head(gapminder_americas_europe))
Code 
gapminder_americas_europe = gapminder_2007.loc[(gapminder_2007['continent'] == "Europe") | (gapminder_2007['continent'] == "Americas")]
gapminder_americas_europe["contEffect"]=0
gapminder_americas_europe["contEffect"].loc[(gapminder_americas_europe['continent'] == "Europe")]=1
gapminder_americas_europe["contEffect"].loc[(gapminder_americas_europe['continent'] == "Americas")]=-1
cols = list(gapminder_americas_europe.columns)
cols = list(gapminder_americas_europe.columns)
cols = cols[len(cols)-1:len(cols):1]+cols[0:-1:1]
gapminder_americas_europe = gapminder_americas_europe[cols]
print(tabulate(gapminder_americas_europe[:6], headers=gapminder_americas_europe.head(), tablefmt="fancy_grid",showindex=False))

Table

Now that we have effect coded the continent, we can create a new model to try to predict an individual’s life expectancy based on which continent they are from

\[ Y = intercept + \beta * effectVariable + Error \]

Which in our case means:

\[ lifeExp = mean(lifeExp) + \beta * contEffect + Error \]

  • Y being the predicted life expectancy.

  • \(\bar{Y}\) being the mean life expectancy regardless of continent. For a t-test this is also the \(intercept\).

  • \(\beta\) being how much to adjust the prediction based on which continent the person is from

  • \(contEffect\) being 1 (Europe) or -1 (Americas) to reflect which continent the participant is from

  • \(Error\) being any error in the prediction not captured by the model

To get the \(intercept\) and \(\beta\) for the above formula let’s use linear model functions:

Code 
continent_ttest <- lm(lifeExp ~ contEffect, gapminder_americas_europe)

continent_ttest$coefficients[1] 
(Intercept) 
   75.62836
Code 
continent_ttest$coefficients[2]
contEffect 
   2.02024
Code 
gapminder_americas_europe$t_fit = continent_ttest$coefficients[1] + # intercept
  continent_ttest$coefficients[2]                       * # gradient
  gapminder_americas_europe$contEffect


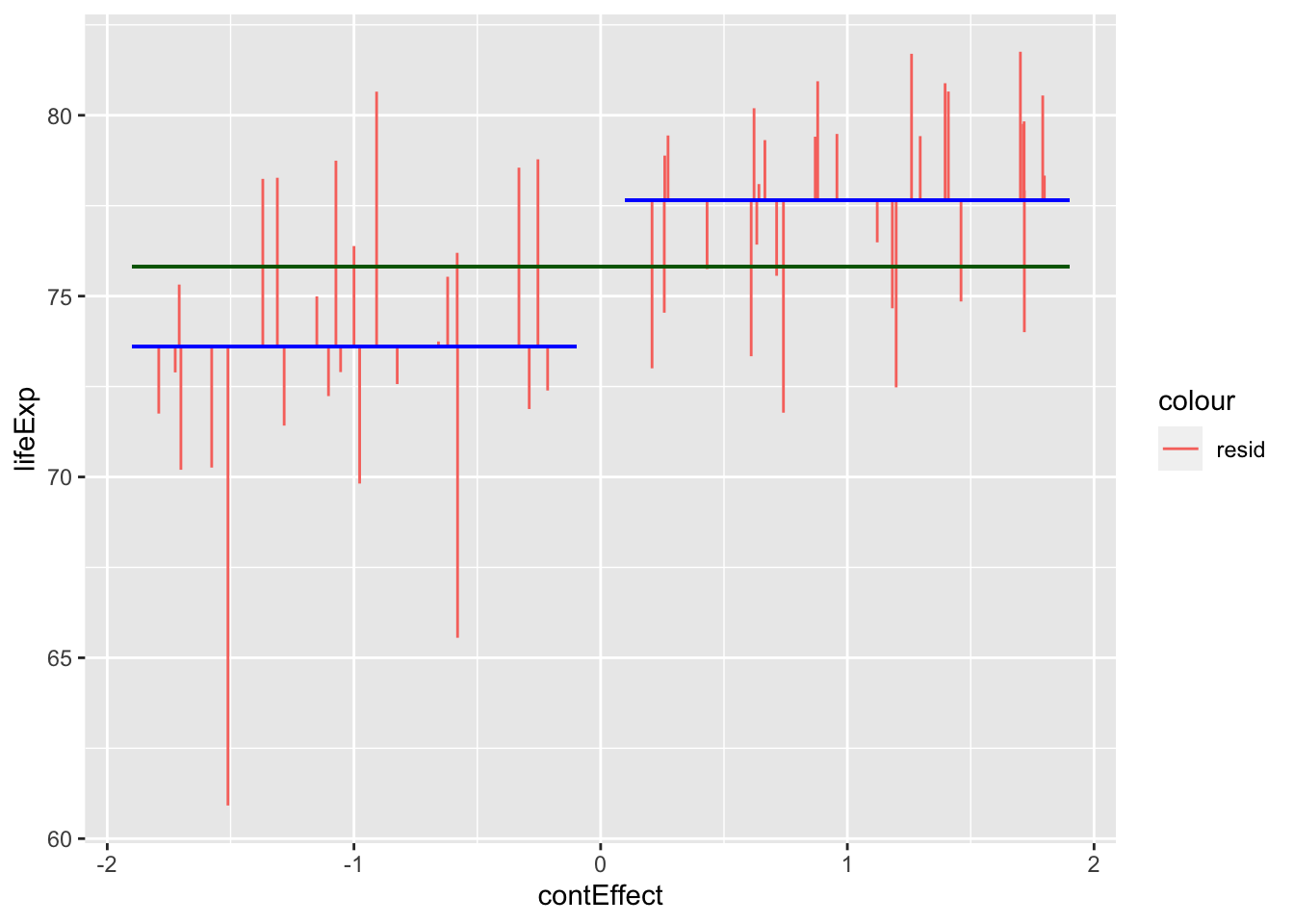
ggplot(gapminder_americas_europe, aes(x = contEffect, y = lifeExp)) +
  geom_segment(
    position = "jitter",
    #arrow = arrow(length = unit(0.01, "npc"),ends = "first"),
    aes(
      xend = contEffect,
      yend = t_fit,
      color = "resid"
    )
  ) + 
  geom_segment(aes(
    x = -1.9, 
    xend = -.1, 
    y = -1 * continent_ttest$coefficients[2] + continent_ttest$coefficients[1],
    yend = -1 * continent_ttest$coefficients[2] + continent_ttest$coefficients[1]),
    color = "blue"
  ) + 
  geom_segment(
    aes(
      x = 0.1, 
      xend = 1.9, 
      y = 1 * continent_ttest$coefficients[2] + continent_ttest$coefficients[1],
      yend = 1 * continent_ttest$coefficients[2] + continent_ttest$coefficients[1]
    ),
    color = "blue"
  ) + 
  geom_segment(
    aes(
      x = - 1.9,
      xend = 1.9,
      y = mean(lifeExp),
      yend = mean(lifeExp)
    ),
    color = "dark green"
  )

Figure 3: Plot with the errors around the mean of life expectancy across Europe and American countries.

Code 
from scipy import stats

# convert 'contEffect' to type category
gapminder_americas_europe['contEffect'] = gapminder_americas_europe['contEffect'].astype('category')

# lm 'contEffect' ~ 'lifeExp'
continent_ttest = stats.linregress(gapminder_americas_europe['contEffect'],gapminder_americas_europe['lifeExp'])

# show results of lm
continent_ttest
LinregressResult(slope=2.020240000000001, intercept=75.62836, rvalue=0.4832076439158285, pvalue=0.00018637488941351192, stderr=0.502794193121279, intercept_stderr=0.5027941931212789)
Code 
gapminder_americas_europe["contEffect"]=0
gapminder_americas_europe["contEffect"].loc[(gapminder_americas_europe['continent'] == "Europe")]=1
gapminder_americas_europe["contEffect"].loc[(gapminder_americas_europe['continent'] == "Americas")]=-1

gapminder_americas_europe['t_fit'] = continent_ttest.intercept +continent_ttest.slope * gapminder_americas_europe['contEffect']

gapminder_americas_europe['t_res_square'] = (gapminder_americas_europe['lifeExp'] - gapminder_americas_europe['t_fit'])**2

# calculate 'lifeExp' mean for 'contEffect' ==-1
m1 = gapminder_americas_europe["lifeExp"][gapminder_americas_europe['contEffect'] == -1].mean()

# calculate 'lifeExp' mean for 'contEffect' ==1
m2 = gapminder_americas_europe["lifeExp"][gapminder_americas_europe['contEffect'] == 1].mean()

# repeat lifeExp' mean for 'contEffect' ==-1
m11=np.repeat(m1, len(gapminder_americas_europe["lifeExp"][gapminder_americas_europe['contEffect'] == -1]), axis=0)

# repeat lifeExp' mean for 'contEffect' ==1
m22=np.repeat(m2, len(gapminder_americas_europe["lifeExp"][gapminder_americas_europe['contEffect'] == 1]), axis=0)

# create x coordinates for 'contEffect' ==-1
x1 = np.arange(-1.98, -.05, 0.08)

# create x coordinates for 'contEffect' ==1
x2 = np.arange(0.05, 1.98, 0.065)


fig, ax = plt.subplots(figsize =(10, 7))
ax.set_ylim([60, 85])
plt.axhline(y=gapminder_americas_europe["lifeExp"].mean(), color='green', ls='-')
plt.hlines(y=m1,xmin=-1.99, xmax=-.04, colors='blue', lw=0.5)
plt.hlines(y=m2,xmin=1.99, xmax=.04, colors='blue', lw=0.5)
plt.vlines(x= x1,ymin=gapminder_americas_europe["lifeExp"][gapminder_americas_europe['contEffect'] == -1], ymax=m11, colors='red', lw=0.5)
plt.vlines(x= x2,ymin=gapminder_americas_europe["lifeExp"][gapminder_americas_europe['contEffect'] == 1], ymax=m22, colors='red', lw=0.5)

# add title on the x-axis
plt.xlabel("contEffect")

# add title on the y-axis
plt.ylabel("lifeExp")

plt.show()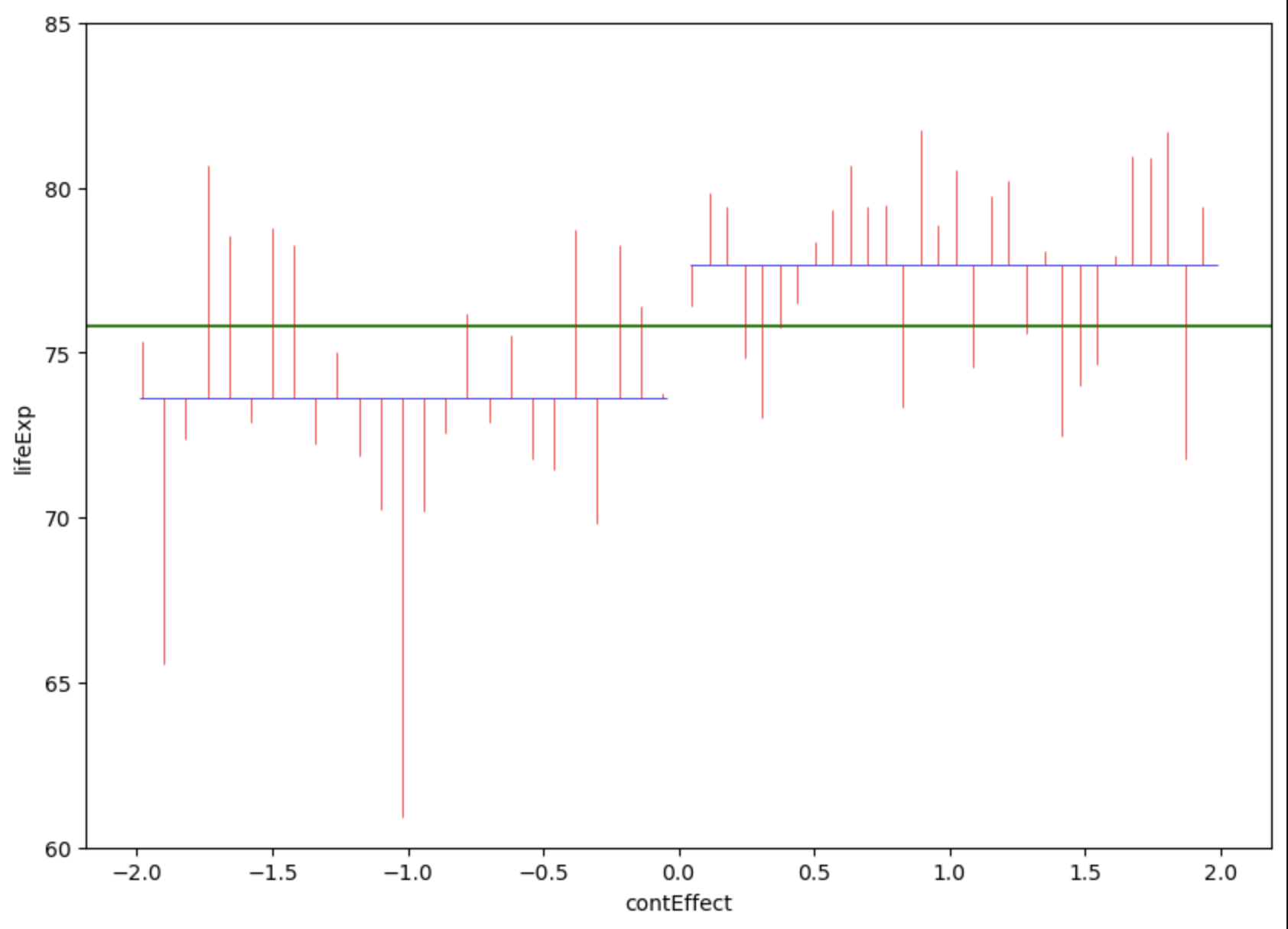

Plot with the errors around the mean of life expectancy across Europe and American countries

Countries in the americas are dummy coded as -1 and countries in Europe are dummy coded as 1. Note that jittering has been used to help visualise variation within continents, and so all countries in Americas had a \(contEffect\) score of -1, even if the jittering above makes it look like participants from Europe had slightly different \(contEffect\) values to each other.

So now that we’ve visualised the predictions and the error, lets summarise these errors with their sum of squares:

Code 
#temp_summary <- summary(lm(lifeExp ~ contEffect, data = gapminder_americas_europe))
summary(aov(lifeExp ~ contEffect, data = gapminder_americas_europe))
            Df Sum Sq Mean Sq F value   Pr(>F)    
contEffect   1  222.6  222.62   16.14 0.000186 ***
Residuals   53  730.8   13.79                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Code 
# between
overall_mean <- mean(gapminder_americas_europe$lifeExp)
europe_mean <- mean(gapminder_americas_europe$lifeExp[gapminder_americas_europe$contEffect == 1])
america_mean <- mean(gapminder_americas_europe$lifeExp[gapminder_americas_europe$contEffect == -1])
ss_between <- 
  sum(gapminder_americas_europe$contEffect == 1) * (europe_mean - overall_mean)^2 +
  sum(gapminder_americas_europe$contEffect == -1) * (america_mean - overall_mean)^2
  
top_half = ss_between

ss_within = (
  sum((gapminder_americas_europe$lifeExp[gapminder_americas_europe$contEffect == 1] - europe_mean)^2) + 
  sum((gapminder_americas_europe$lifeExp[gapminder_americas_europe$contEffect == -1] - america_mean)^2)
)
  
bottom_half = (ss_within/(length(gapminder_americas_europe$lifeExp) - 2))

top_half/bottom_half
[1] 16.14453
Code 
# Compare with a t-test

t.test(
  gapminder_americas_europe$lifeExp[gapminder_americas_europe$contEffect == 1],
  gapminder_americas_europe$lifeExp[gapminder_americas_europe$contEffect == -1],
  var.equal = T
)

    Two Sample t-test

data:  gapminder_americas_europe$lifeExp[gapminder_americas_europe$contEffect == 1] and gapminder_americas_europe$lifeExp[gapminder_americas_europe$contEffect == -1]
t = 4.018, df = 53, p-value = 0.0001864
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 2.023525 6.057435
sample estimates:
mean of x mean of y 
 77.64860  73.60812
Code 
4.018^2
[1] 16.14432
Code 
# look at a t-distribution compared to an f-distribution
Code 
import statsmodels.api as sm
from statsmodels.formula.api import ols

# create the model
model = ols('lifeExp ~ contEffect', data = gapminder_americas_europe).fit()

# create a table for the model
aov_table = sm.stats.anova_lm(model, typ=2)

# display the table
aov_table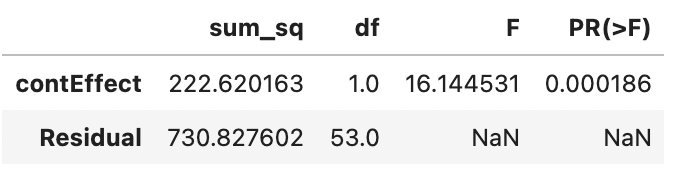

Table

Code 
# between
overall_mean = gapminder_americas_europe['lifeExp'].mean()
europe_mean = gapminder_americas_europe['lifeExp'][gapminder_americas_europe['contEffect'] == 1].mean()

america_mean = gapminder_americas_europe['lifeExp'][gapminder_americas_europe['contEffect'] == -1].mean()

ss_between =(sum(gapminder_americas_europe['contEffect'] == 1) * (europe_mean - overall_mean)**2) + (sum(gapminder_americas_europe['contEffect'] == -1) * (america_mean - overall_mean)**2)

top_half = ss_between

ss_within = (sum((gapminder_americas_europe['lifeExp'][gapminder_americas_europe['contEffect'] == 1] - europe_mean)**2)+ sum((gapminder_americas_europe['lifeExp'][gapminder_americas_europe['contEffect'] == -1] - america_mean)**2))

bottom_half = (ss_within/(len(gapminder_americas_europe['lifeExp']) - 2))

top_half/bottom_half
16.14453
Code 
# Compare with a t-test
from scipy.stats import ttest_ind

t_test = ttest_ind(gapminder_americas_europe['lifeExp'][gapminder_americas_europe['contEffect'] == 1],gapminder_americas_europe['lifeExp'][gapminder_americas_europe['contEffect'] == -1])
t_test
Ttest_indResult(statistic=4.018025720342183, pvalue=0.00018637488941352037)
Code 
4.018 ** 2
16.144530689331322

So the new unexplained variance (AKA residual) is 730.8276, which is smaller than it was when we just used the mean regardless of continent (953.4478; 935.4478 is also the total variance around the mean).

The sum of squares for the effect of continent can be calculated by subtracting the residuals from the total sum of squares (SS):

\[ effect_{SS} = total_{SS} - residual_{SS} = 953.4478 - 730.8276 = 222.6202 \]

The \(effect_{SS}\) can also be thought of our explained variance! So we can actually calculate how much of the model is explained by the model (\(r^2\)):

\[ r^2 = \frac{SS_{explained}}{SS_{total}} = \frac{222.6202}{953.4478} = 0.2335 \]

Let’s confirm that this is correct by comparing a manual calculation and a function:

Code 
222.6202/953.4478 # should be  0.2335 
[1] 0.2334897
Code 
summary(lm(lifeExp ~ contEffect, gapminder_americas_europe))$r.squared
[1] 0.2334896
Code 
222.6202/953.4478
0.23348965722087775
Code 
# create the model
model = ols('lifeExp ~ contEffect', data = gapminder_americas_europe).fit()

# get the r squared from the model
r_squared = model.rsquared

# Print the R-squared value
print("R-squared:", r_squared)
0.2334896271386857

Great, the difference reflects a rounding error.

Note that the above formula is similar to the formula for \(r\) from simple regressions. Variance is the square root of the Sum of Squares (or Sum of Squares is the square of variance!):

\[ r = \sqrt{\frac{SS_{explained}}{SS_{total}}} = \frac{\sqrt{SS_{explained}}}{\sqrt{SS_{total}}} =\frac{var_{explained}}{var_{total}} \]

ANOVA approach vs conventional formula

The main formula for an independent samples t-test is:

\[ t = \frac{\bar{X_1} - \bar{X_2}}{SE} \]

However, this is a simplification of the GLM mathematics we’ve been doing above (although \(df\) is the same for the denominator and numerator, so we ignored them as they cancelled out)

\[ t= \sqrt{f} = \sqrt{\frac{SS_{exp}/df_{exp}}{SS_{unexp}/df_{unexp}}} = \frac{(\sum{\bar{X_1} - \mu)/(N_1-1) - (\sum{\bar{X_2} - \mu)}/(N_2-1)}}{ ((\sum{X_{1i} - \bar{X_1}}) + (\sum{X_{2i} - \bar{X_2}}) )/(N-1)}= \frac{\sum{\bar{X_1}/N_1 - \sum{\bar{X_2}}/N_2}}{SE} = \frac{\bar{X_1} - \bar{X_2}}{SE} \]

GLM approach (optional)

If we were to more strictly conceptualise this as a linear model, then we need to create a model that predicts the life expectancy based on the continent. As continent is a categorical variable, we need to allocate numbers for each continent. This can either be dummy coding (1 for 0 for each continent) or effect coding (1 or -1 for each continent). Let’s go through both approaches.

Dummy coding

In this model, we will dummy code America as 1 and Europe as 0. This means that our model will tell us how much life expectancy increases/decreases when you live in America compared to Europe. A general linear model with 1 predictor is generally structured as follows:

\[ Y = a + B*X + e \]

Or in relation to our variables

\[ GDP = a + B_{continent} * X_{continent} + e = \]

  • \(X\) refers to the value of our dummy coded variable, which is either 0 (Europe) or 1 (Americas).

  • \(a\) is the intercept, i.e. the value of \(Y\) when \(X = 0\). Thus, as \(X=0\) for Europe, \(a\) is the mean life expectancy in Europe. This will be clarified below.

  • \(B\) is the gradient (AKA Coefficient AKA Beta) of the predictor. In our case, this will be the difference in means between Europe and the Americas, which will be further clarified below.

  • \(e\) is the error, or residual (i.e. the difference between the predicted value and the actual value).

So it’s been claimed that \(a\) will be the mean life expectancy in Europe. We can see why this is the case by seeing what happens when \(X=0\), which follows our dummy coding of Europe as 0.

\[ LifeExp = a + B_{continent} * 0 + e = a + e \]

So predicting GDP for Europe is just \(a\) and whatever is not predicted by \(a\) is the error (\(e\)). The best prediction of GDP in Europe is calculating the mean of life expectancy in Europe. Thus \(a\) is the mean life expectancy in Europe.

Now, to get the gradient (\(B\)), we need to calculate how much life expectancy goes up or down as \(X\) increases by 1.

Code 
gapminder_americas_europe
   contEffect                country continent year lifeExp       pop gdpPercap
1           1                Albania    Europe 2007  76.423   3600523  5937.030
2          -1              Argentina  Americas 2007  75.320  40301927 12779.380
3           1                Austria    Europe 2007  79.829   8199783 36126.493
4           1                Belgium    Europe 2007  79.441  10392226 33692.605
5          -1                Bolivia  Americas 2007  65.554   9119152  3822.137
6           1 Bosnia and Herzegovina    Europe 2007  74.852   4552198  7446.299
7          -1                 Brazil  Americas 2007  72.390 190010647  9065.801
8           1               Bulgaria    Europe 2007  73.005   7322858 10680.793
9          -1                 Canada  Americas 2007  80.653  33390141 36319.235
10         -1                  Chile  Americas 2007  78.553  16284741 13171.639
11         -1               Colombia  Americas 2007  72.889  44227550  7006.580
12         -1             Costa Rica  Americas 2007  78.782   4133884  9645.061
13          1                Croatia    Europe 2007  75.748   4493312 14619.223
14         -1                   Cuba  Americas 2007  78.273  11416987  8948.103
15          1         Czech Republic    Europe 2007  76.486  10228744 22833.309
16          1                Denmark    Europe 2007  78.332   5468120 35278.419
17         -1     Dominican Republic  Americas 2007  72.235   9319622  6025.375
18         -1                Ecuador  Americas 2007  74.994  13755680  6873.262
19         -1            El Salvador  Americas 2007  71.878   6939688  5728.354
20          1                Finland    Europe 2007  79.313   5238460 33207.084
21          1                 France    Europe 2007  80.657  61083916 30470.017
22          1                Germany    Europe 2007  79.406  82400996 32170.374
23          1                 Greece    Europe 2007  79.483  10706290 27538.412
24         -1              Guatemala  Americas 2007  70.259  12572928  5186.050
25         -1                  Haiti  Americas 2007  60.916   8502814  1201.637
26         -1               Honduras  Americas 2007  70.198   7483763  3548.331
27          1                Hungary    Europe 2007  73.338   9956108 18008.944
28          1                Iceland    Europe 2007  81.757    301931 36180.789
29          1                Ireland    Europe 2007  78.885   4109086 40675.996
30          1                  Italy    Europe 2007  80.546  58147733 28569.720
31         -1                Jamaica  Americas 2007  72.567   2780132  7320.880
32         -1                 Mexico  Americas 2007  76.195 108700891 11977.575
33          1             Montenegro    Europe 2007  74.543    684736  9253.896
34          1            Netherlands    Europe 2007  79.762  16570613 36797.933
35         -1              Nicaragua  Americas 2007  72.899   5675356  2749.321
36          1                 Norway    Europe 2007  80.196   4627926 49357.190
37         -1                 Panama  Americas 2007  75.537   3242173  9809.186
38         -1               Paraguay  Americas 2007  71.752   6667147  4172.838
39         -1                   Peru  Americas 2007  71.421  28674757  7408.906
40          1                 Poland    Europe 2007  75.563  38518241 15389.925
41          1               Portugal    Europe 2007  78.098  10642836 20509.648
42         -1            Puerto Rico  Americas 2007  78.746   3942491 19328.709
43          1                Romania    Europe 2007  72.476  22276056 10808.476
44          1                 Serbia    Europe 2007  74.002  10150265  9786.535
45          1        Slovak Republic    Europe 2007  74.663   5447502 18678.314
46          1               Slovenia    Europe 2007  77.926   2009245 25768.258
47          1                  Spain    Europe 2007  80.941  40448191 28821.064
48          1                 Sweden    Europe 2007  80.884   9031088 33859.748
49          1            Switzerland    Europe 2007  81.701   7554661 37506.419
50         -1    Trinidad and Tobago  Americas 2007  69.819   1056608 18008.509
51          1                 Turkey    Europe 2007  71.777  71158647  8458.276
52          1         United Kingdom    Europe 2007  79.425  60776238 33203.261
53         -1          United States  Americas 2007  78.242 301139947 42951.653
54         -1                Uruguay  Americas 2007  76.384   3447496 10611.463
55         -1              Venezuela  Americas 2007  73.747  26084662 11415.806
      t_fit
1  77.64860
2  73.60812
3  77.64860
4  77.64860
5  73.60812
6  77.64860
7  73.60812
8  77.64860
9  73.60812
10 73.60812
11 73.60812
12 73.60812
13 77.64860
14 73.60812
15 77.64860
16 77.64860
17 73.60812
18 73.60812
19 73.60812
20 77.64860
21 77.64860
22 77.64860
23 77.64860
24 73.60812
25 73.60812
26 73.60812
27 77.64860
28 77.64860
29 77.64860
30 77.64860
31 73.60812
32 73.60812
33 77.64860
34 77.64860
35 73.60812
36 77.64860
37 73.60812
38 73.60812
39 73.60812
40 77.64860
41 77.64860
42 73.60812
43 77.64860
44 77.64860
45 77.64860
46 77.64860
47 77.64860
48 77.64860
49 77.64860
50 73.60812
51 77.64860
52 77.64860
53 73.60812
54 73.60812
55 73.60812

Effect coding

Calculating p-values from t-distributions

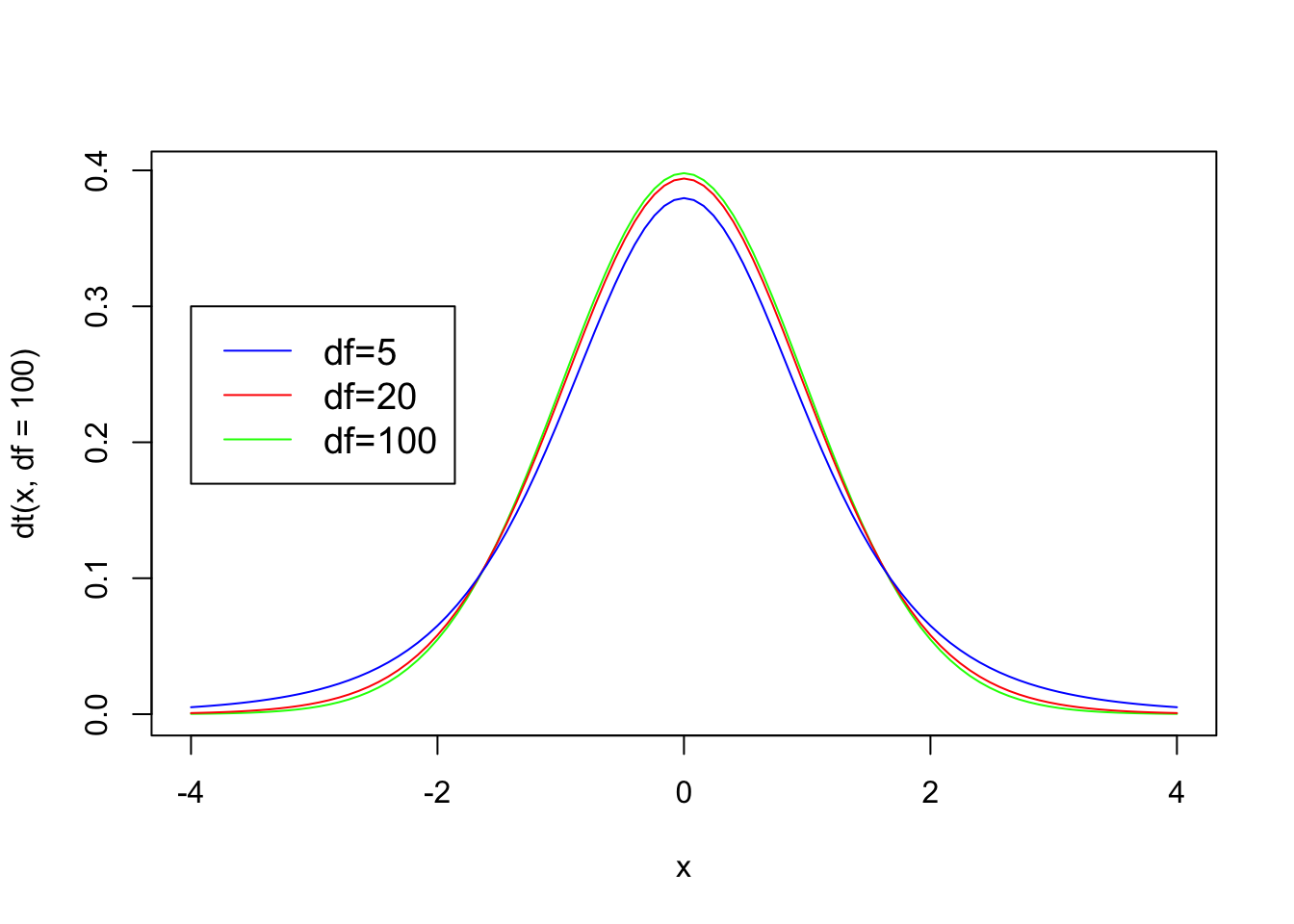
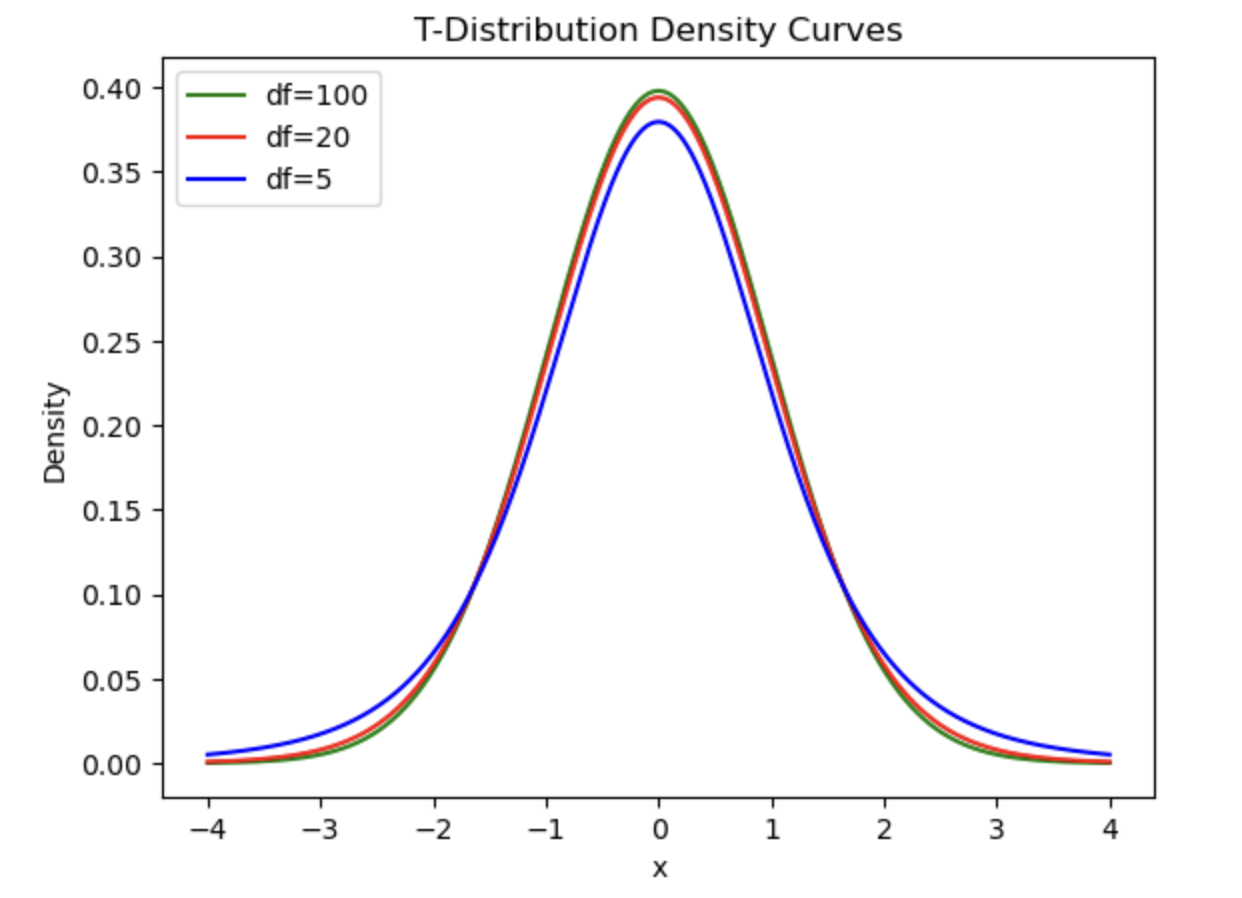
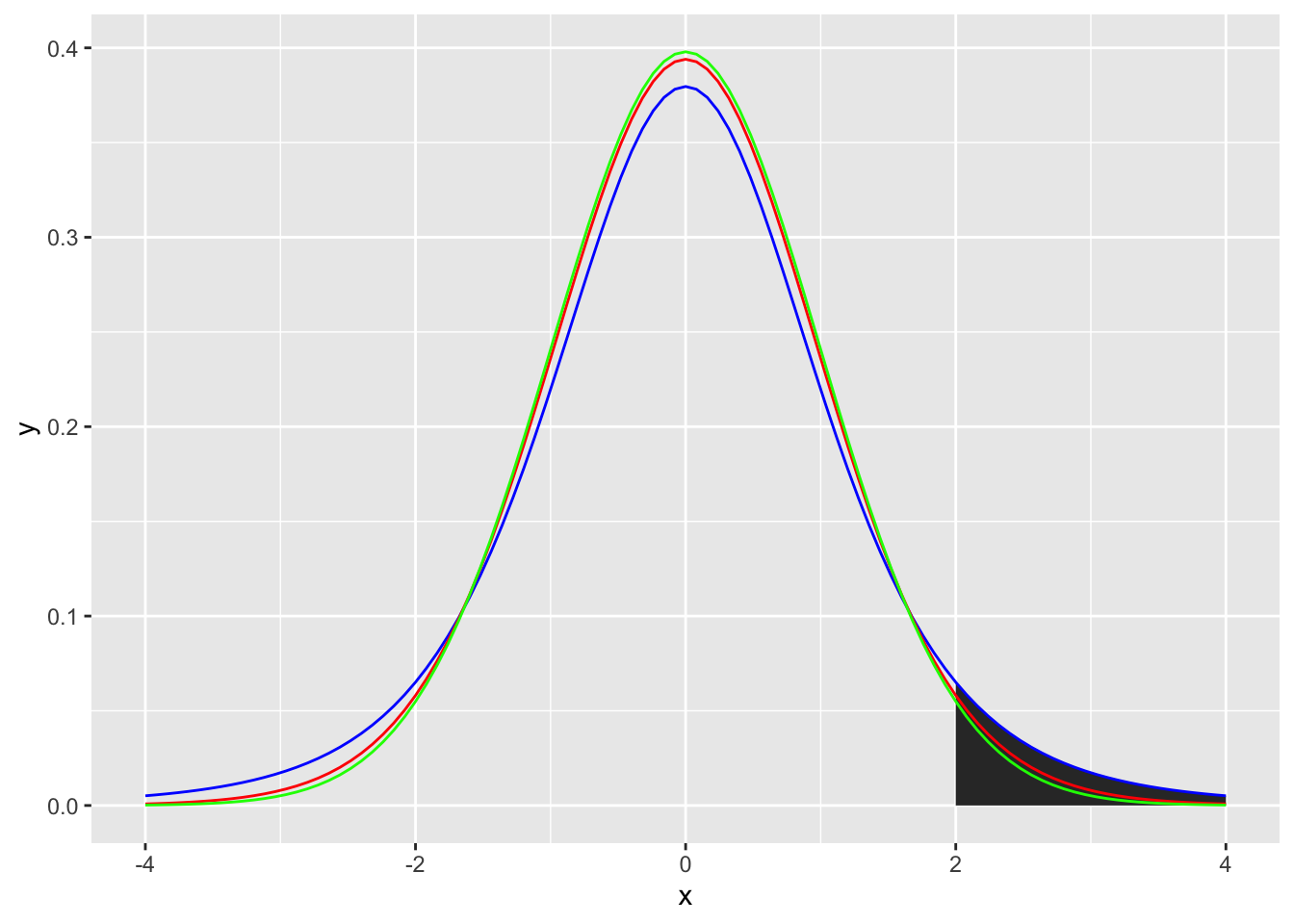
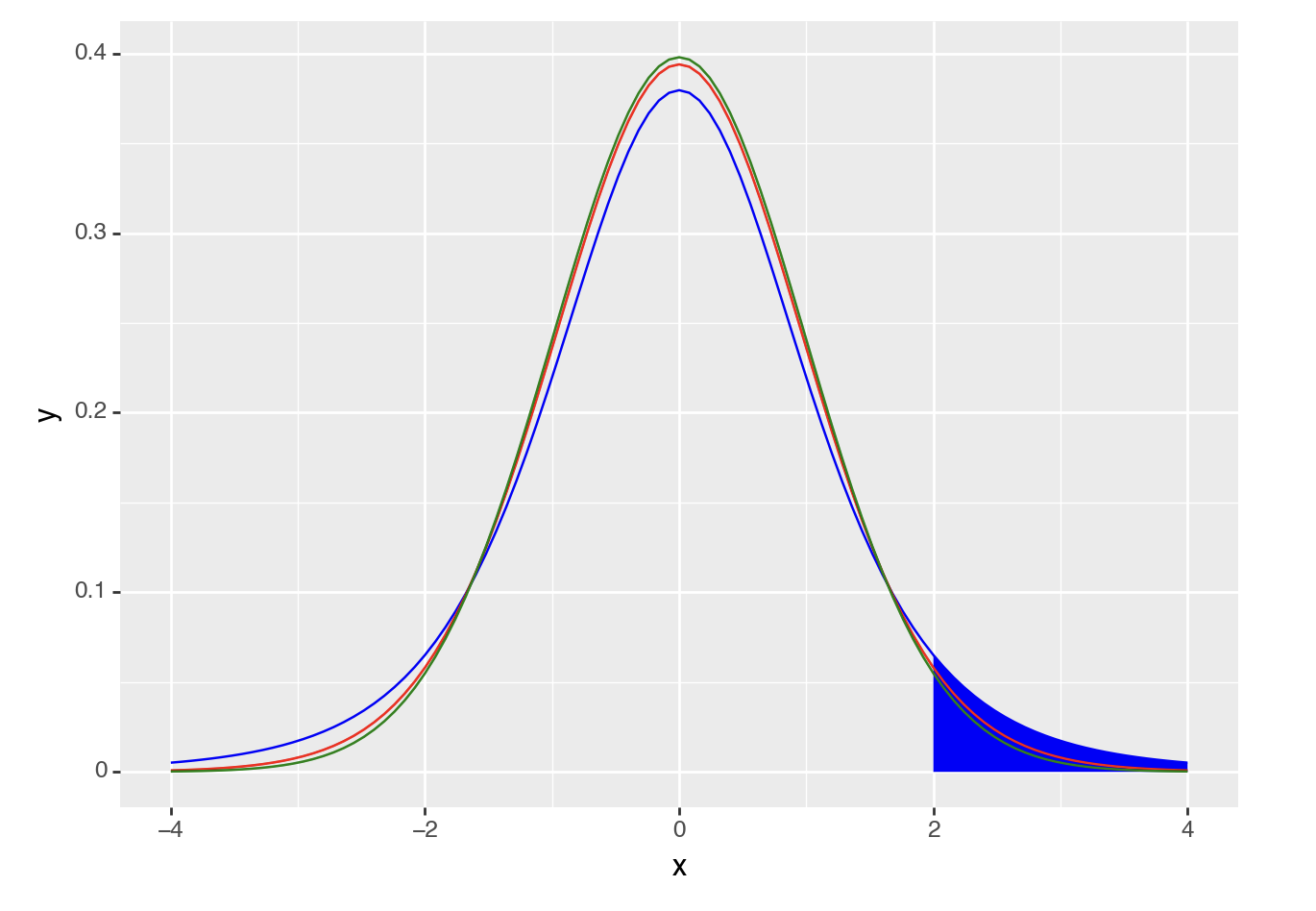
Similar to the normal distribution, we can calculate how likely it is that you would get a t-value or higher (or lower) by drawing a t-distribution that represents the likelihood of getting any t-value. For example, if you wanted to calculate the likelihood of getting a t-value of 2 or higher you could generate a figure as follows (note the area under the curve):

Code 
ggplot(data.frame(x = c(-4, 4)), aes(x)) +
  stat_function(fun = dt,   args =list(df =5), xlim = c(2,4), geom = "area") + 
  stat_function(fun = dt, args =list(df =5), color = "blue")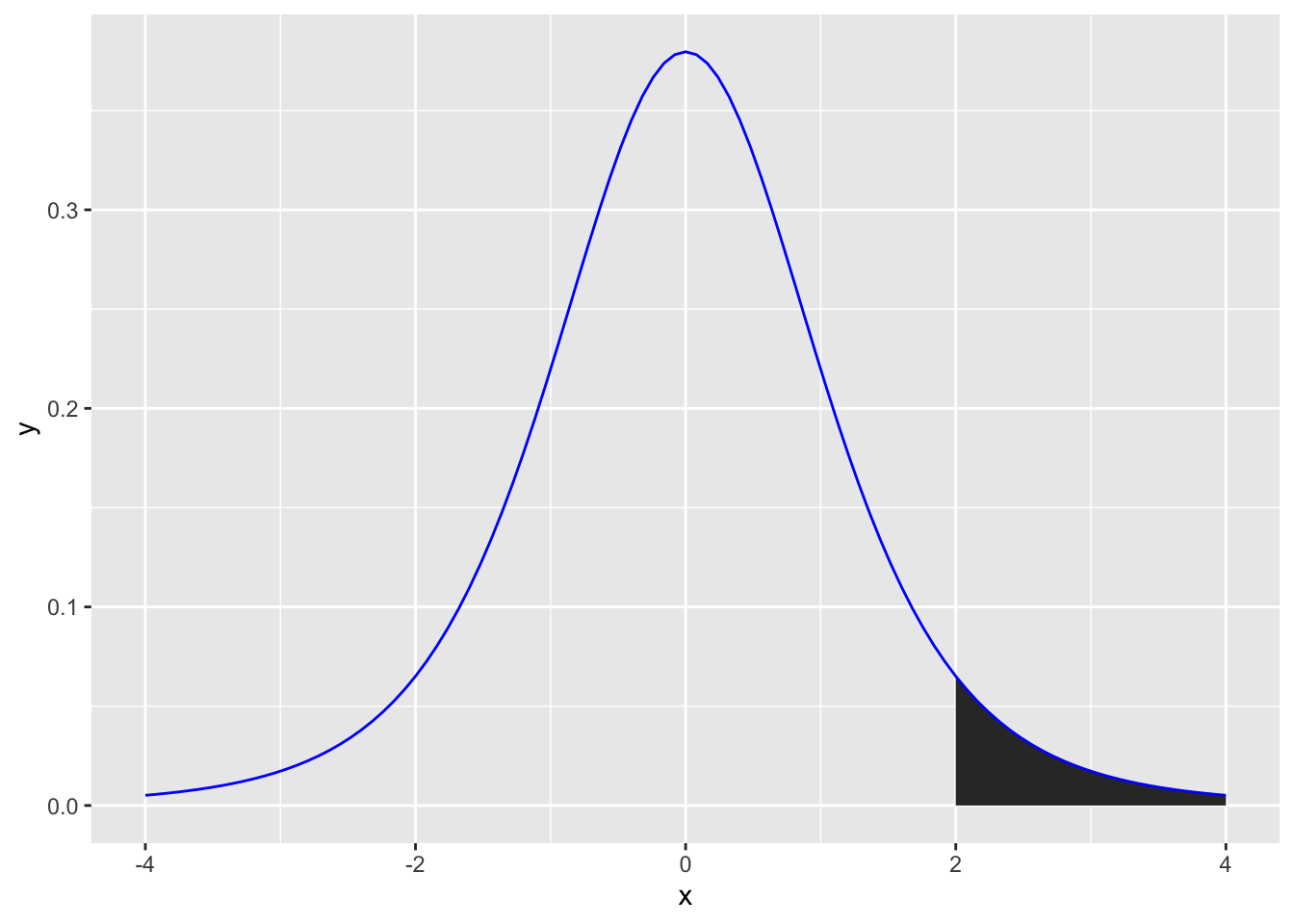

A t-distribution reflects the likelihood of getting a particular t-value if the null hypothesis is correct. So the most likely t-value you will get is 0. It’s equally likely that you will get a positive and negative t-value, so the distribution will be symmetrical. The bell shape reflects how data clusters around a mean (same as for a normal distribution).

A t-distribution is like a normal distribution (it’s a bell curve), but also takes into account the number of participants (or data points) using degrees of freedom (N-1). Here are the t-distributions you would get for 101, 21 and 6 participants:

Code 
curve(dt(x, df=100), from=-4, to=4, col='green')
curve(dt(x, df=20), from=-4, to=4, col='red', add=TRUE)
curve(dt(x, df=5), from=-4, to=4, col='blue', add = TRUE) 

#add legend
legend(-4, .3, legend=c("df=5", "df=20", "df=100"),
       col=c("blue", "red", "green"), lty=1, cex=1.2)

Code 
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import t

# Define the x values
x = np.linspace(-4, 4, 1000)

# Create density curves for different degrees of freedom
plt.plot(x, t.pdf(x, df=100), color='green', label='df=100')
plt.plot(x, t.pdf(x, df=20), color='red', label='df=20')
plt.plot(x, t.pdf(x, df=5), color='blue', label='df=5')

# Add a legend
plt.legend(loc='upper left')

# Set axis labels and plot title
plt.xlabel('x')
plt.ylabel('Density')
plt.title('T-Distribution Density Curves')

# Show the plot
plt.show()

T-Distribution Density Curves’

We can see that the slopes get steeper the higher the \(df\) is (i.e. the more participants you have). This means that the results become more significant even with the same t-value. Not convinced? Let’s use a t-value of 2 to illustrate this. In the following figure you can see that the area under the curve for a t-value of 2 or more gets visually smaller the more participants/the higher the \(df\) value is:

Code 
ggplot(data.frame(x = c(-4, 4)), aes(x)) +
  stat_function(fun = dt,   args =list(df =5), xlim = c(2,4), geom = "area") + 
  stat_function(fun = dt, args =list(df =5), color = "blue") +
  stat_function(fun = dt, args =list(df =20), color = "red") +
  stat_function(fun = dt, args =list(df =100), color = "green")

Code 
from plotnine import ggplot, aes, stat_function, xlim, geom_area, geom_line
from scipy.stats import t

import pandas as pd

# Define the data frame with x values
df = pd.DataFrame({'x': [-4, 4]})

# Create the  plot
(
    ggplot(df, aes(x='x'))
    + stat_function(fun=lambda x: t.pdf(x, df=5), geom="area", xlim=(2, 4), fill="blue")
    + stat_function(fun=lambda x: t.pdf(x, df=5), color="blue")
    + stat_function(fun=lambda x: t.pdf(x, df=20), color="red")
    + stat_function(fun=lambda x: t.pdf(x, df=100), color="green")
)

Figure with the area under the curve for a t-value of 2’

Remember, area under the curve IS the p-value, so the area under the curve for a t-value of 2 or above for each degrees of freedom is:

Code 
# area under the curve for 2 and above
pt(
  # t-value
  q=2, 
  # degrees of freedom
  df=5, 
  # is the test of the t-value and below (TRUE) or the t-value and above (FALSE)
  lower.tail = FALSE
)
[1] 0.05096974
Code 
pt(
  # t-value
  q=2, 
  # degrees of freedom
  df=20, 
  # is the test of the t-value and below (TRUE) or the t-value and above (FALSE)
  lower.tail = FALSE
)
[1] 0.02963277
Code 
pt(
  # t-value
  q=2, 
  # degrees of freedom
  df=100, 
  # is the test of the t-value and below (TRUE) or the t-value and above (FALSE)
  lower.tail = FALSE
)
[1] 0.02410609
Code 
from scipy.stats import t

# t-value
t_value = 2

# Degrees of freedom
df = 5

# Calculate the area under the curve for t >= 2
area_above_2 = 1 - t.cdf(t_value, df=df)
area_above_2
0.050969739414929105
Code 
# t-value
t_value = 2

# Degrees of freedom
df = 20

# Calculate the area under the curve for t >= 2
area_above_2 = 1 - t.cdf(t_value, df=df)
area_above_2
0.02963276772328527
Code 
# t-value
t_value = 2

# Degrees of freedom
df = 100

# Calculate the area under the curve for t >= 2
area_above_2 = 1 - t.cdf(t_value, df=df)
area_above_2
0.024106089365566796

Note that if you wanted a 2-tailed test (i.e. you didn’t have an expected direction of your finding) you would double the area under the curve/p-value.

Similar principles apply for an F-distribution, described next.

Calculating p-values from F-distributions

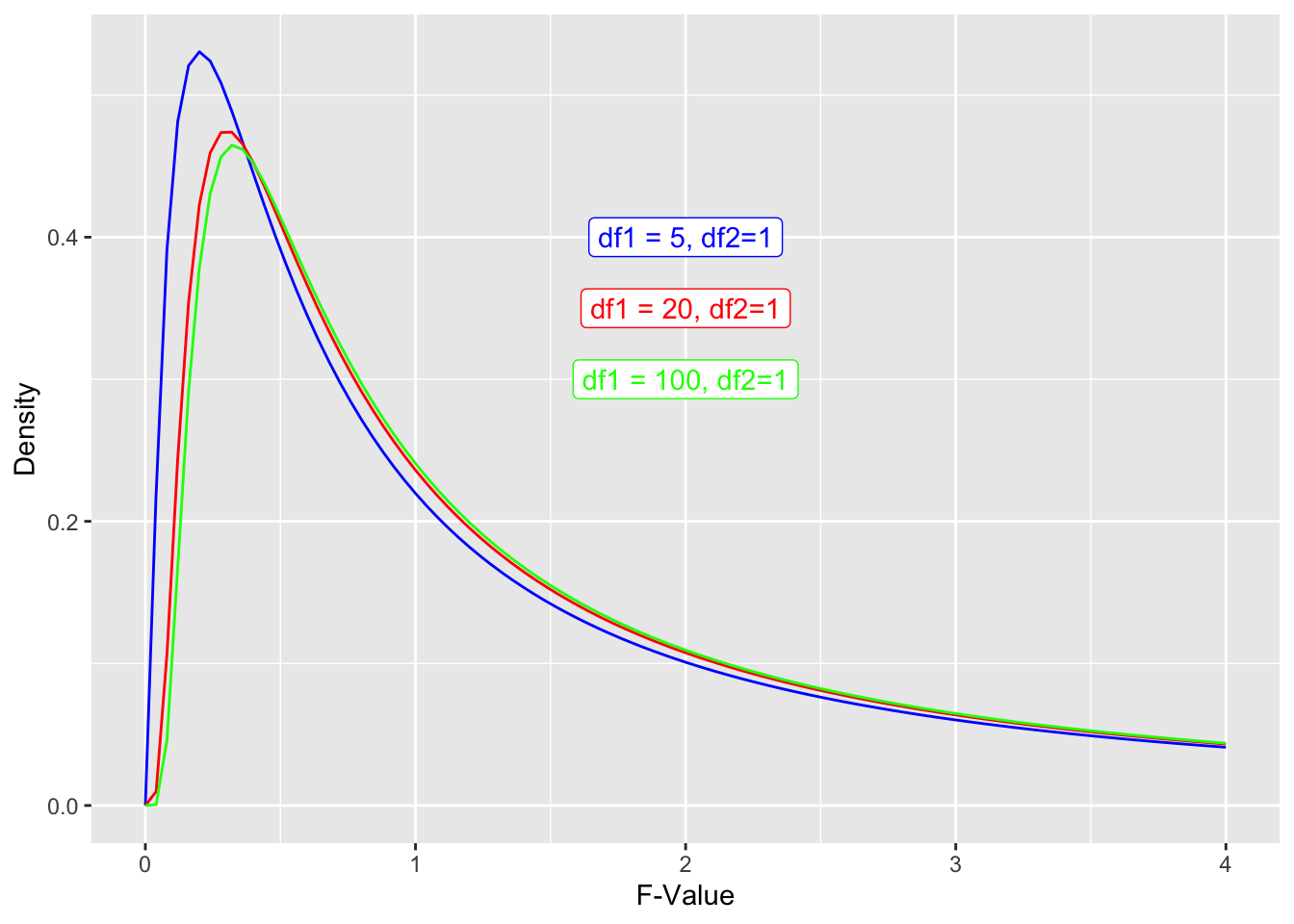
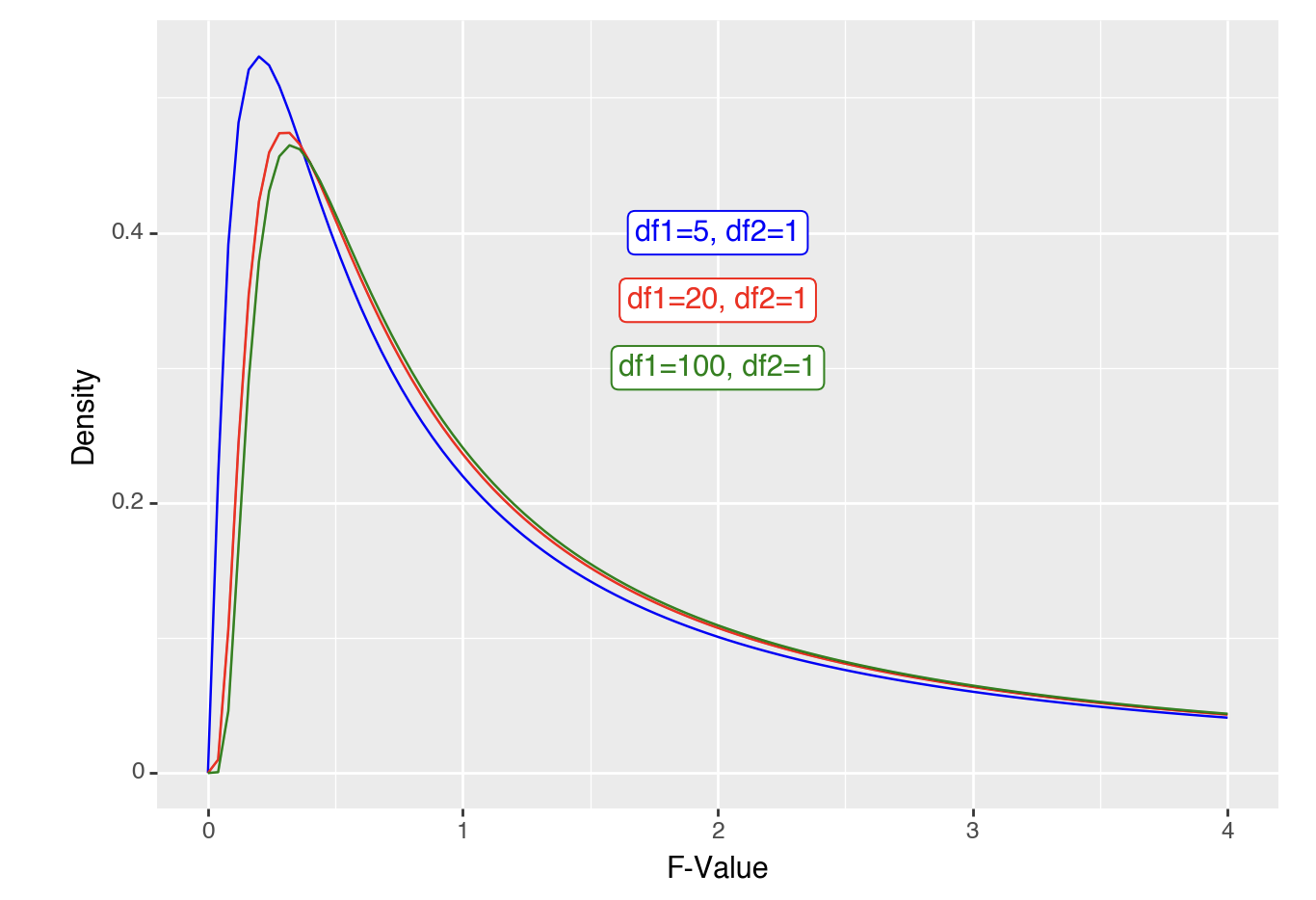
As F-values are based on the sum of squares, which are always positive, they cannot be negative. Also, F distributions can reflect more complex designs than t-distributions. Put together, the distributions are not symmetrical. However, the principle of calculating an F-value and comparing it to an F-distribution to get a p-value is the same as for t-values above. For example, if you wanted to calculate the likelihood of getting an F-value of 2 or higher you would calculate the area under the curve for an F-distribution (note the highlighted area):

Code 
ggplot(data.frame(x = c(0, 4)), aes(x)) +
  stat_function(fun = df, args =list(df1 =5, df2=1), xlim = c(2,4), geom = "area") + 
  stat_function(fun = df, args =list(df1 =5, df2=1), color = "blue")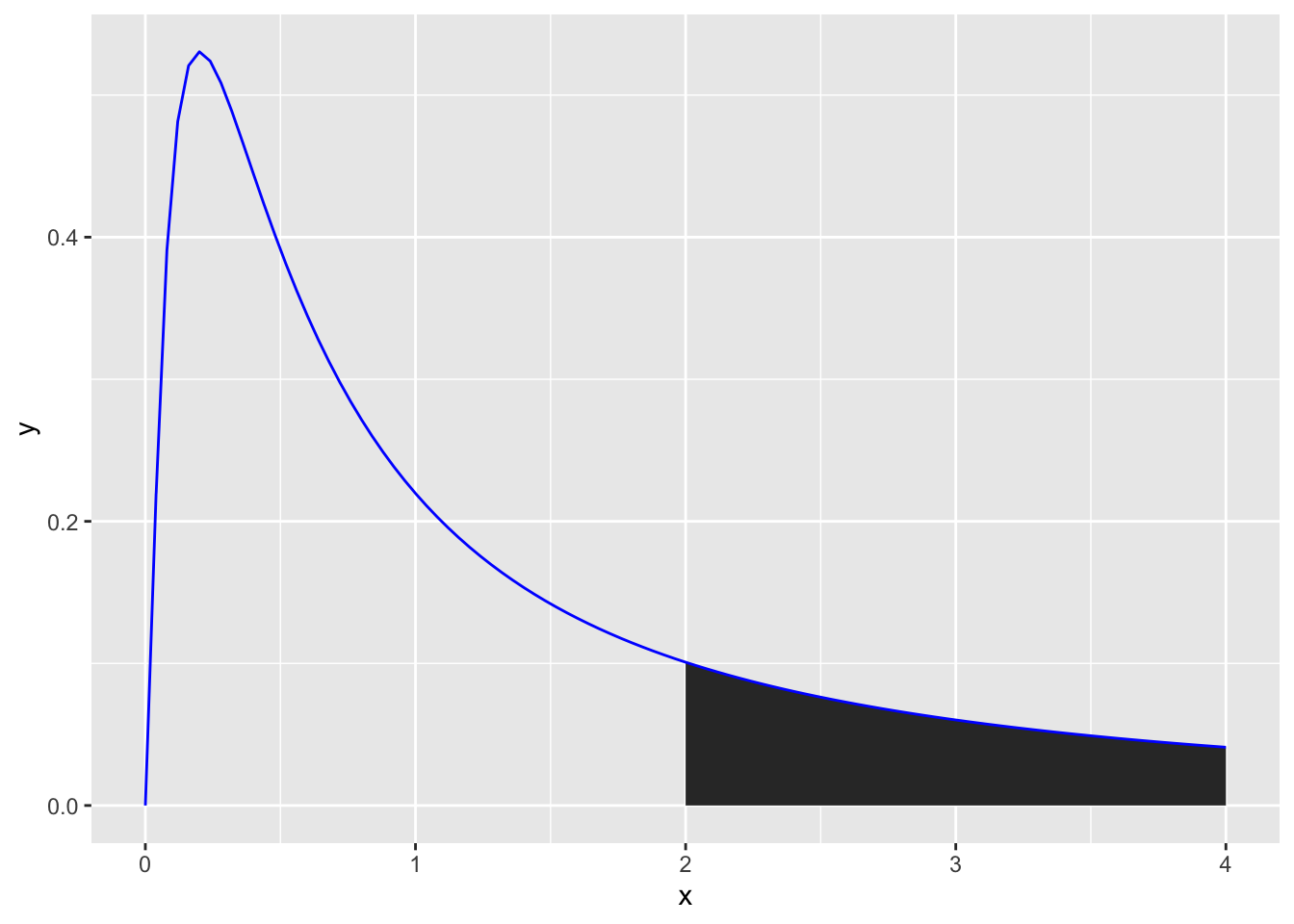

The shape of F-distributions is influenced by having both explained and unexplained degrees of freedom. This means that they can have a variety of shapes to reflect these differences in degrees of freedom. First, let’s look at some distributions for designs with 2 conditions but differing numbers of participants:

Code 
ggplot(data.frame(x = c(0, 4)), aes(x)) +
  # stat_function(fun = df, args =list(df1 =5, df2=1), xlim = c(2,4), geom = "area") + 
  stat_function(fun = df, args =list(df1 =5, df2=1), color = "blue") +
  stat_function(fun = df, args =list(df1 =20, df2=1), color = "red") +
  stat_function(fun = df, args =list(df1 =100, df2=1), color = "green") +
  annotate("label", x = 2, y = .4, label = "df1 = 5, df2=1", colour="blue") +
  annotate("label", x = 2, y = .35, label = "df1 = 20, df2=1", colour="red") +
  annotate("label", x = 2, y = .3, label = "df1 = 100, df2=1", colour="green") +
  xlab("F-Value") +
  ylab("Density")

Code 
import pandas as pd
from plotnine import ggplot, aes, stat_function, annotate, labs
from scipy.stats import f

# Create a DataFrame with x values
df = pd.DataFrame({'x': [0, 4]})

# Create the plot
(
    ggplot(df, aes(x='x'))
    + stat_function(
        fun=lambda x: f.pdf(x, dfn=5, dfd=1),
        color='blue'
    )
    + stat_function(
        fun=lambda x: f.pdf(x, dfn=20, dfd=1),
        color='red'
    )
    + stat_function(
        fun=lambda x: f.pdf(x, dfn=100, dfd=1),
        color='green'
    )
    + annotate(
        "label", x=2, y=0.4, label="df1=5, df2=1", color="blue"
    )
    + annotate(
        "label", x=2, y=0.35, label="df1=20, df2=1", color="red"
    )
    + annotate(
        "label", x=2, y=0.3, label="df1=100, df2=1", color="green"
    )
    + labs(x="F-Value", y="Density")
)

F-Distribution Density Curves’

The shape is roughly the same, but shifts slightly as you get more people. What happens if we look at distributions where there are about 100 people but 2 or more conditions (df2 = 2 or more).

Code 
ggplot(data.frame(x = c(0, 4)), aes(x)) +
  # stat_function(fun = df, args =list(df1 =5, df2=1), xlim = c(2,4), geom = "area") + 
  stat_function(fun = df, args =list(df1 =100, df2=1), color = "blue") +
  stat_function(fun = df, args =list(df1 =100, df2=2), color = "red") +
  stat_function(fun = df, args =list(df1 =100, df2=3), color = "green") +
  annotate("label", x = 2, y = .4, label  = "df1 = 100, df2=1", colour="blue") +
  annotate("label", x = 2, y = .35, label = "df1 = 100, df2=2", colour="red") +
  annotate("label", x = 2, y = .3, label  = "df1 = 100, df2=3", colour="green") +
  xlab("F-Value") +
  ylab("Density")

Code 
from plotnine import ggplot, aes, stat_function, annotate, labs

# Create a DataFrame with x values
df = pd.DataFrame({'x': [0, 4]})

# Create the plot
(
    ggplot(df, aes(x='x'))
    + stat_function(
        fun=lambda x: f.pdf(x, dfn=100, dfd=1),
        color='blue'
    )
    + stat_function(
        fun=lambda x: f.pdf(x, dfn=100, dfd=2),
        color='red'
    )
    + stat_function(
        fun=lambda x: f.pdf(x, dfn=100, dfd=3),
        color='green'
    )
    + annotate(
        "label", x=2, y=0.4, label="df1=100, df2=1", color="blue"
    )
    + annotate(
        "label", x=2, y=0.35, label="df1=100, df2=2", color="red"
    )
    + annotate(
        "label", x=2, y=0.3, label="df1=100, df2=3", color="green"
    )
    + labs(x="F-Value", y="Density")
)

F-Distribution Density Curves’

In all cases, you get your p-value from calculating the area under the curve for that F-value or above.

Effect sizes

T-tests

To capture how large the effect is, there are slightly different calculations when doing a within subject design (1 or 2 conditions that all participants complete) vs. a between subject design. In all cases these are Cohen \(d\) calculations.

One Sample T-tests

The size of an effect is how big the difference is between the mean and the \(\mu\) that you are comparing it to, compared to the standard deviation:

\[ d = \frac{\bar{x} - \mu}{SD(x)} \]

The general benchmarks for how big or small a Cohen’s \(d\) value are as follows:

Paired sample T-tests

The size of an effect is how big the difference is between the conditions, compared to the standard deviation:

\[ d = \frac{\bar{x_1} - \bar{x_2}}{SD(x_1-x_2)} \]

This actually can be thought of the same as one-sample t-tests after you take the step to calculate the difference between each value in \(x_1\) and \(x_2\) to make \(x_3\) to compare to a \(\mu\) of 0:

\[ x_3 = x_1 - x_2 \] \[ \mu = 0 \] \[ d = \frac{\bar{x_1}-\bar{x_2}}{SD(\bar{x_1}-\bar{x_2})} = \frac{\bar{x_3}}{SD(x_3)} = \frac{\bar{x_3}-\mu}{SD(x_3)} \]

Independent Sample T-tests

The formula for this is somewhat similar to that for a paired samples t-test, but because you are comparing between groups of participants you can’t collapse the values between conditions because there are no pairings. So, you need to calculate the pooled standard deviation.

\[ SD_{pooled} = \sqrt{(SD(x_1)^2 + SD(x_1)^2)/2} \]

\[ d = \frac{\bar{x_1}-\bar{x_2}}{SD_{pooled}} \]

F-tests

The effect sizes for F-tests are based on how much variance is explained by the model, which sometimes is exactly the same as \(r^2\). Let’s review some of the calculations above to confirm this:
\[ r^2 = \frac{SS_{explained}}{SS_{total}} = \frac{222.6202}{953.4478} = 0.2335 \]

If we run a linear model on the data we should also confirm the \(r^2\) is .2335:

Code 
summary(lm(lifeExp ~ contEffect, gapminder_americas_europe))

Call:
lm(formula = lifeExp ~ contEffect, data = gapminder_americas_europe)

Residuals:
     Min       1Q   Median       3Q      Max 
-12.6921  -2.1364   0.4494   2.5671   7.0449 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  75.6284     0.5028 150.416  < 2e-16 ***
contEffect    2.0202     0.5028   4.018 0.000186 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.713 on 53 degrees of freedom
Multiple R-squared:  0.2335,    Adjusted R-squared:  0.219 
F-statistic: 16.14 on 1 and 53 DF,  p-value: 0.0001864
Code 
import statsmodels.api as sm
import statsmodels.formula.api as smf

# Create the model
model = smf.ols('lifeExp ~ contEffect', data=gapminder_americas_europe)
results = model.fit()

# Print the summary
print(results.summary())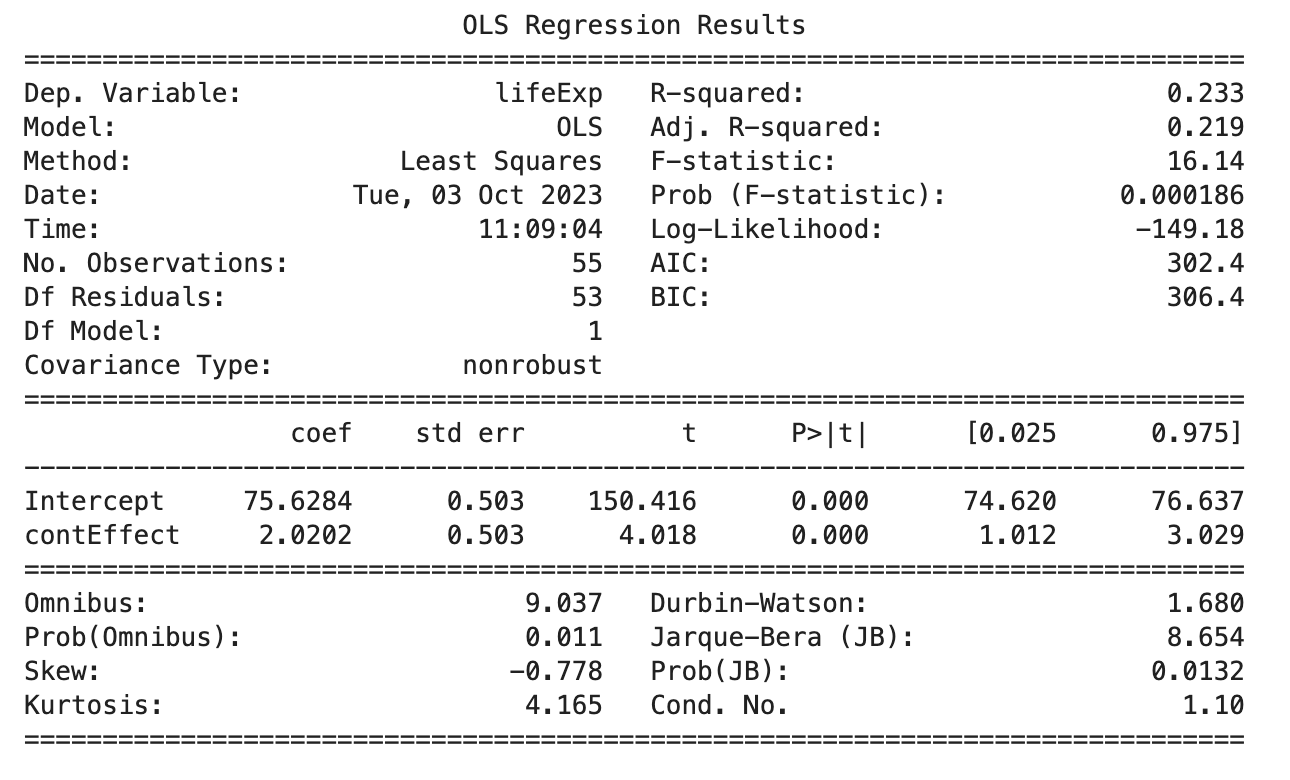

Table

We’ll use a function to confirm that this is the same for eta squared also:

Code 
lsr::etaSquared(lm(lifeExp ~ contEffect, gapminder_americas_europe))
              eta.sq eta.sq.part
contEffect 0.2334896   0.2334896
Code 
import statsmodels.api as sm
import statsmodels.formula.api as smf
from statsmodels.stats.anova import anova_lm

# Create the model
model = smf.ols('lifeExp ~ contEffect', data=gapminder_americas_europe)
results = model.fit()

# Calculate eta-squared
anova_table = anova_lm(results)
eta_squared = anova_table['sum_sq'][0] / (anova_table['sum_sq'][0] + anova_table['sum_sq'][1])

print("Eta-squared (η²):", eta_squared)
Eta-squared (η²): 0.2334896271386854

Boom, you got effect sizes for F-tests like ANOVAs.

If you have understood this page it will set you up for the pages on each type of ANOVA as it uses the same concepts again and again.